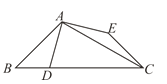
题目内容
【题目】如图,在平面直角坐标系中,已知A(0,5), B(a,b),且a,b满足b=![]() +
+![]() -1.
-1.
(1)如图,求线段AB的长;
(2)如图,直线CD与x轴、y轴正半轴分别交于点C,D,∠OCD=45°,第四象限的点P(m,n)在直线CD上,且mn=-6,求OP2-OC2的值;
(3)如图,若点D(1,0),求∠DAO +∠BAO的度数.
【答案】(1)![]() ;(2)12 ;(3)45°
;(2)12 ;(3)45°
【解析】
(1)根据b=![]() +
+![]() -1可求得a、b的值,得到B点的坐标,根据两点间坐标公式即可求解.
-1可求得a、b的值,得到B点的坐标,根据两点间坐标公式即可求解.
(2)根据直线CD与x轴、y轴正半轴分别交于点C,D,∠OCD=45°,可知直线CD平行于y= -x,可设直线CD解析式为y= -x +b,代入P点坐标,得到m、n、b的关系,代入计算即可.
(3)取点D关于y轴的对称点![]() ,运用两点间坐标公式及勾股定理逆定理可判断△AB
,运用两点间坐标公式及勾股定理逆定理可判断△AB![]() 是等腰直角三角形,即可求得∠BA
是等腰直角三角形,即可求得∠BA![]() 的值,等量代换即可.
的值,等量代换即可.
(1)∵b=![]() +
+![]() -1
-1
∴a=4 ,b= -1
∴B点坐标为:(4,-1)
∵A(0,5)
∴AB=![]() )
)![]()
(2)∵直线CD与x轴、y轴正半轴分别交于点C,D,∠OCD=45°
∴直线CD平行于y= -x
设直线CD解析式为y= -x +b
则B点坐标为(b,0)
把点P(m,n)代入得:n= -m +b
∴b= m+n
∴OP2-OC2=![]()
∵mn=-6
∴OP2-OC2![]()
(3)取点D关于y轴的对称点![]() ,则∠DAO=∠
,则∠DAO=∠![]() ,
,
∴∠DAO +∠BAO=∠![]() +∠BAO=∠BA
+∠BAO=∠BA![]()
∵点D(1,0)
∴![]() (-1,0)
(-1,0)
由(1)得:A(0,5),B(4,-1)
∴A![]() =
=![]() ,
,![]() ,
,![]()
∴A![]() ,
,![]()
∴△A![]() 是等腰直角三角形
是等腰直角三角形
∴∠DAO +∠BAO=∠BA![]() =45°
=45°

【题目】探究逼近![]() 的有理近似值.
的有理近似值.
方法介绍:
经过![]() 步操作(
步操作(![]() 为正整数)不断寻找有理数
为正整数)不断寻找有理数![]() ,
,![]() ,使得
,使得![]() ,并且让
,并且让![]() 的值越来越小,同时利用数轴工具将任务几何化,直观理解通过等分线段的方法不断缩小
的值越来越小,同时利用数轴工具将任务几何化,直观理解通过等分线段的方法不断缩小![]() 对应的点
对应的点![]() 所在线段的长度(二分法)
所在线段的长度(二分法)
思路
在数轴上记![]() ,
,![]() 对应的点分别为
对应的点分别为![]() ,
,![]() 和
和![]() 的平均数
的平均数![]() 对应线段
对应线段![]() 的中点(记为
的中点(记为![]() ).通过判断
).通过判断![]() 还是
还是![]() ,得到点
,得到点![]() 是在二等分后的“左线段
是在二等分后的“左线段![]() ”上还是“右线段
”上还是“右线段![]() ”上,重复上述步骤,不断得到
”上,重复上述步骤,不断得到![]() ,从而得到
,从而得到![]() 更精确的近似值.
更精确的近似值.
具体操作步骤及填写“阅读活动任务单”:
(1)当![]() 时,
时,
①寻找左右界值:先寻找两个连续正整数![]() ,使得
,使得![]() .
.
因为![]() ,所以
,所以![]() ,那么
,那么![]() ,
,![]() ,线段
,线段![]() 的中点
的中点![]() 对应的数
对应的数![]() .
.
②二分定位:判断点![]() 在“左线段
在“左线段![]() ”上还是在“右线段
”上还是在“右线段![]() ”上.
”上.
比较7与![]() 的大小,从而确定
的大小,从而确定![]() 与
与![]() 的大小;
的大小;
因为![]() >
> ![]() (填 “>”或“<”),得到点
(填 “>”或“<”),得到点![]() 在线段
在线段 ![]() 上(填“
上(填“![]() ”或“
”或“![]() ”).
”).
(2)当![]() 时,在(1)中所得
时,在(1)中所得![]() 的基础上,仿照以上步骤,继续进行下去,得到表中
的基础上,仿照以上步骤,继续进行下去,得到表中![]() 时的相应内容.
时的相应内容.
请继续仿照以上步骤操作下去,补全“阅读活动任务单”:
|
|
|
|
| 点 | 得出更精确的 |
1 | 2 | 3 | 2.5 |
| 点 |
|
2 | 2.5 | 3 | 2.75 |
| 点 |
|
3 | 2.5 | 2.75 | 2.625 |
| ||
4 |