题目内容
如图,BD为⊙O的直径,AB=AC,AD交BC于点E.

1.①求证:△ABE∽△ADB;②若AE=2,ED=4,求⊙O的面积
2.延长DB到F,使得,连接FA,若AC∥FD,试判断直线FA与⊙O的位置关系,并说明理由.
1.![]()
2.直线FA与⊙O相切
解析:(1) ①![]() AB=AC
AB=AC![]() ∠ABC=∠ADC
∠ABC=∠ADC
![]() ∠BAD=∠BAE
∠BAD=∠BAE
![]() △ABE∽△ADB
△ABE∽△ADB
②![]() △ABE∽△ADB
△ABE∽△ADB
![]()
![]()
![]() AB=
AB=![]()
![]() BD为⊙O的直径
BD为⊙O的直径
![]() △ADB是直角三角形
△ADB是直角三角形
BD=![]() =
=![]()
S=![]() =
=![]() .
.
(2) 直线FA与⊙O相切。
![]() AC∥FD
AC∥FD
![]() ∠BDA=∠CBD
∠BDA=∠CBD
![]() ∠BDA=∠CBD=∠ABC
∠BDA=∠CBD=∠ABC
![]() ∠BDA=30°
∠BDA=30°
![]() ∠BOA=60°
∠BOA=60°
![]() BO=AO,BF=BO
BO=AO,BF=BO
![]() AB=
AB=![]() FO
FO
![]() △AOF是直角三角形,
△AOF是直角三角形,
![]() ∠0AF=90°
∠0AF=90°
![]() 直线FA与⊙O相切
直线FA与⊙O相切

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 10、如图,一电线杆AB的影子分别落在了地上和墙上,某一时刻,小明竖起1米高的直杆,量得其影长为0.5米,此时,他又量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.小明用这些数据很快算出了电线杆AB的高.请你计算,电线杆AB的高为( )
10、如图,一电线杆AB的影子分别落在了地上和墙上,某一时刻,小明竖起1米高的直杆,量得其影长为0.5米,此时,他又量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.小明用这些数据很快算出了电线杆AB的高.请你计算,电线杆AB的高为( )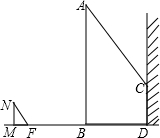 如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?
如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗? (2012•渝北区一模)如图,等边△ABC的边AB与正方形DEFG的边长均为2,且AB与DE在同一条直线上,开始时点B与点D重合,让△ABC沿这条直线向右平移,直到点B与点E重合为止,设BD的长为x,△ABC与正方形DEFG重叠部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
(2012•渝北区一模)如图,等边△ABC的边AB与正方形DEFG的边长均为2,且AB与DE在同一条直线上,开始时点B与点D重合,让△ABC沿这条直线向右平移,直到点B与点E重合为止,设BD的长为x,△ABC与正方形DEFG重叠部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
