题目内容
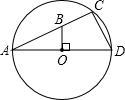如图，AD、AC分别是直径和弦，∠CAD=30°，B是AC上一点，BO⊥AD，垂足为O，BO=5cm，则CD等于________cm．
5
分析：在直角△ACD中，依据直角三角形的性质：30度的锐角所对的直角边等于斜边的一半即可求得AB的长，然后利用勾股定理即可求得半径OA的长度，则直径AD即可求得，然后在直角△ACD中，依据30度的锐角所对的直角边等于斜边的一半即可求解．
解答：∵在直角△AOB中∠CAD=30°，
∴AB=2OB=2×5=10cm，
AO=
=5cm．
∴AD=2AO=10cm．
∵AD是圆的直径，
∴∠C=90°，
又∵∠CAD=30°，
∴CD=
AD=×10=5（cm）．
故答案是：5．
点评：本题考查了圆周角定理以及直角三角形的性质：30度的锐角所对的直角边等于斜边的一半，理解定理是关键．
分析：在直角△ACD中，依据直角三角形的性质：30度的锐角所对的直角边等于斜边的一半即可求得AB的长，然后利用勾股定理即可求得半径OA的长度，则直径AD即可求得，然后在直角△ACD中，依据30度的锐角所对的直角边等于斜边的一半即可求解．
解答：∵在直角△AOB中∠CAD=30°，
∴AB=2OB=2×5=10cm，
AO=
=5cm．∴AD=2AO=10
cm．∵AD是圆的直径，
∴∠C=90°，
又∵∠CAD=30°，
∴CD=
AD=×10=5（cm）．故答案是：5
．点评：本题考查了圆周角定理以及直角三角形的性质：30度的锐角所对的直角边等于斜边的一半，理解定理是关键．
练习册系列答案
相关题目
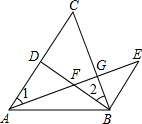已知：如图，D是AC上一点，BE∥AC，BE=AD，AE分别交BD、BC于点F、G，∠1=∠2．
如图，AD是△ABC的中线，E、F分别在AB、AC上，且DE⊥DF 求证：BE+CF＞EF．
