题目内容
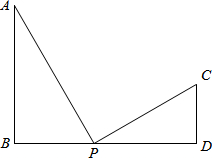
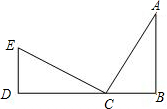如图，已知AB⊥BD，ED⊥BD垂足分别是点B，点D，点C在BD上，AB=CD，BC=ED，则∠ACE=________．
90°
分析：由题中条件可得Rt△ABC≌Rt△CDE，再通过角之间的转化，进而可得出结论．
解答：∵AB⊥BD，ED⊥BD，
∴∠D=∠B=90°，
∵在Rt△ABC和Rt△CDE中
，
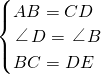∴Rt△ABC≌Rt△CDE（SAS），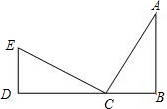
∴∠DCE=∠A，
∵∠B=90°，
∴∠BAC+∠ACB=90°，
∴∠ECD+∠ACB=90°，
∴∠ACE=180°-90°=90°．
故此题答案为90°．
点评：本题主要考查了全等三角形的判定及性质，能够熟练掌握．
分析：由题中条件可得Rt△ABC≌Rt△CDE，再通过角之间的转化，进而可得出结论．
解答：∵AB⊥BD，ED⊥BD，
∴∠D=∠B=90°，
∵在Rt△ABC和Rt△CDE中
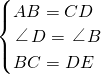，∴Rt△ABC≌Rt△CDE（SAS），
∴∠DCE=∠A，
∵∠B=90°，
∴∠BAC+∠ACB=90°，
∴∠ECD+∠ACB=90°，
∴∠ACE=180°-90°=90°．
故此题答案为90°．
点评：本题主要考查了全等三角形的判定及性质，能够熟练掌握．
练习册系列答案
同步练习强化拓展系列答案
相关题目
9、如图，已知AB⊥BD，ED⊥BD，C是BD上一点，AB=CD，BC=ED，那么下列结论中，不正确的是（ ）
49、如图，已知AB⊥BD，垂足为B，ED⊥BD，垂足为D，AB=CD，BC=DE，则∠ACE=
（2013•永州）如图，已知AB⊥BD，CD⊥BD
如图，已知AB⊥BD，BC⊥CD，AD=a，CD=b，则BD的长的取值范围为（ ）