题目内容
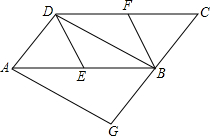 已知:如图,在?ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
已知:如图,在?ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.(1)写出图中所有的全等三角形,并证明其中任意一对三角形全等;
(2)如果四边形BFDE是菱形,那么四边形AGBD是什么特殊四边形?并证明你的结论.
考点:平行四边形的性质,全等三角形的判定与性质,菱形的性质,矩形的判定
专题:
分析:(1)利用平行四边形的性质结合全等三角形的判定方法得出即可;
(2)利用平行四边形的性质结合全等三角形的判定与性质得出△CDB≌△BAG进而求出即可.
(2)利用平行四边形的性质结合全等三角形的判定与性质得出△CDB≌△BAG进而求出即可.
解答:解:(1)△ADE≌△CBF,△DEB≌△BFD,△ABD≌△CDB,
△ABD≌△BAG,△CDB≌△BAG;
证明△ADE≌△CBF,
理由:∵四边形ABCD是平行四边形,
∴AD=BC,AB=DC,∠DAE=∠C,
∵E、F分别为边AB、CD的中点,
∴CF=AE,
在△ADE和△CBF中
,
∴△ADE≌△CBF(SAS);
(2)四边形AGBD是矩形.
理由:连接EF,
∵四边形BFDE是菱形,
∴BE=DF.
∴EF⊥BD.
∴∠DOE=90°.
又∵四边形ABCD是平行四边形,
∴AB∥DC.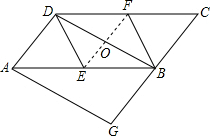
∵点E是AB的中点,
∴AE=EB.
∴AE=DF.
∴四边形ADEF是平行四边形.
∴AD∥EF.
∴∠ADB=90°.
∵AB∥CD,
∴∠C=∠ABG.
同理:∠G=∠DBC.
在△CDB和△BAG中,
,
∴△CDB≌△BAG(AAS).
∴AG=BD.
∴四边形AGBD是平行四边形.
∵∠ADB=90°,
∴四边形AGBD是矩形.
△ABD≌△BAG,△CDB≌△BAG;
证明△ADE≌△CBF,
理由:∵四边形ABCD是平行四边形,
∴AD=BC,AB=DC,∠DAE=∠C,
∵E、F分别为边AB、CD的中点,
∴CF=AE,
在△ADE和△CBF中
|
∴△ADE≌△CBF(SAS);
(2)四边形AGBD是矩形.
理由:连接EF,
∵四边形BFDE是菱形,
∴BE=DF.
∴EF⊥BD.
∴∠DOE=90°.
又∵四边形ABCD是平行四边形,
∴AB∥DC.

∵点E是AB的中点,
∴AE=EB.
∴AE=DF.
∴四边形ADEF是平行四边形.
∴AD∥EF.
∴∠ADB=90°.
∵AB∥CD,
∴∠C=∠ABG.
同理:∠G=∠DBC.
在△CDB和△BAG中,
|
∴△CDB≌△BAG(AAS).
∴AG=BD.
∴四边形AGBD是平行四边形.
∵∠ADB=90°,
∴四边形AGBD是矩形.
点评:此题主要考查了平行四边形的性质以及全等三角形的判定与性质等知识,熟练应用全等三角形判定方法是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知a=|-12+2|,则a的相反数是( )
| A、-4 | B、-3 | C、-1 | D、0 |
下列图形中,既是轴对称图形又是中心对称图形的是( )
| A、等腰三角形 | B、菱形 |
| C、平行四边形 | D、直角三角形 |
 如图,已知AB∥CD,说明∠ABE、∠BED、∠CDE有怎样的数量关系.
如图,已知AB∥CD,说明∠ABE、∠BED、∠CDE有怎样的数量关系. 如图,AB是线段CD的垂直平分线,E,F是AB上的两点,求证:∠ECF=∠EDF.
如图,AB是线段CD的垂直平分线,E,F是AB上的两点,求证:∠ECF=∠EDF.