题目内容
如图1,在直角梯形ABCD中,AD//BC,∠A=90°,AB=8cm,AD=6cm, BC=10cm。点P从点B出发沿BD方向匀速运动,速度为1cm/s;同时,线段EF从CD出发沿DA方向匀速运动,速度为1 cm/s,且EF与BD交于点Q,连接PE、PF。当点P与点Q相遇时,所有运动停止。若设运动时间为t(s).
(1)求CD的长度
(2)当PE//AB时,求t的值;
(3)①设△PEF的面积为S,求S关于t的函数关系式;
②如图2,当△PEF的外接圆圆心O恰好在EF中点时,则t的值为 (请直接写出答案)
(1)过点D作DM⊥BC,交BC于点M
∵AD//BC,∠A=90°
∴ DM=AB=8cm,BM=AD=6cm
∴CM="4cm,"
∴CD= cm
cm
(2)由题意可求BD=10cm,BP=t,
∴DP="10-t" DE=t
∵PE//CD
∴△DPE∽△DBA
∴ 即
即
解得t=

(3)①过点B作BH⊥CD,交于点H,过点P作PG⊥EF,交于点G,
∵BD=BC=10cm,CD= cm
cm
∴DH= cm
cm
∴BH= cm
cm
∵EF//CD 易证, EF=CD= ,DQ=DE=t,
,DQ=DE=t,
∴QP=BD-BP-DQ=10-2t
可证 △QPG∽△DBH
∴ 即
即 ∴PG=
∴PG=
S=
② t=

提示:如图过点P作MN//AB,则PM⊥AD,PN⊥BC
由题意可知∠EPF=90°
通过相似可得PM= PN=
PN=
ME== NF==
NF==


由 可解得t1=
可解得t1= ,t2=
,t2= (舍去) (也可用相似法)
(舍去) (也可用相似法)
解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
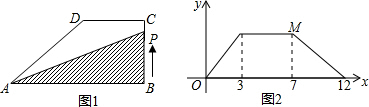
 如图1,在直角梯形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )
如图1,在直角梯形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )| A、3 | B、4 | C、5 | D、6 |