Question

如图，四边形ABCD为正方形．点A的坐标为(0，2)，点B的坐标为（0，-3）．反比例函数y₁=图象经过点C，一次函数y₂ =ax+b的图象经过点A、C

    (1)求反比例函数与一次函数的解析式；

    (2)观察图象，在第四项限内写出使得y₁<y₂成立的自变量x的取值范围;

    (3)若点P是反比例函数图象上的一点，且△OAP的面积恰好等于正方形ABCD的面积，求P点的坐标，

Answer 1

解：(1)∵点A的坐标为(0.2)，点B的坐标为(0，-3)．∴AB=5．

 ∵四边形ABCD为正方形，∴点C的坐标为(5，- 3).

 ∵反比例函数y=的图象经过点C，

 ∴一3=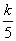，解得k= -15,∴反比例函数的解析式为y=-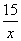；……（2分）

 ∵一次函数的解析式为y=ax+b的图像经过点A，C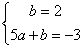，∴，解得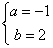

∴一次函数的解析式为y=-x+2；…………（4分）（2）0<x<5………………（6分）

  (3)设P点的坐标为(x，y)．∵△OAP的面积恰好等于正方形ABCD的面积，

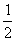  ∴×OA·|x|=5²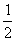，∴×2|x| =25，解得x=±25．

  当x=25时，y=-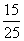=-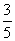；当x=-25时．Y==

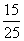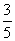
 ∴P点的坐标为(25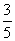，-)或(-25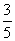，)．……(9分)