题目内容
已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
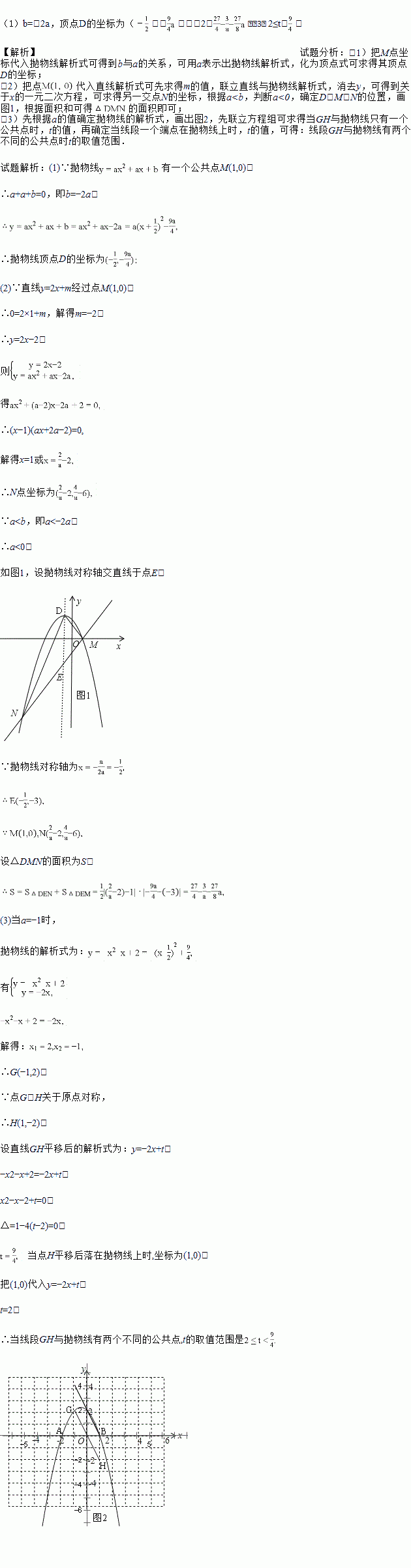
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.
练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
根据下表,确定方程ax2+bx+c=0的一个解的取值范围是( )
x | 2 | 2.23 | 2.24 | 2.25 |
ax2+bx+c | ﹣0.05 | ﹣0.02 | 0.03 | 0.07 |
A. 2<x<2.23 B. 2.23<x<2.24 C. 2.24<x<2.25 D. 2.24<x≤2.25

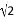 的相反数是( )
的相反数是( )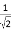 B.
B. 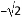 C.
C. 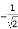 D.
D. 
 B.
B.  C.
C.  D.
D. 
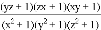 的值.
的值.
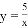 的图象上有三点A(﹣2,y1)、B(﹣1,y2)、C(2,y3),则( )
的图象上有三点A(﹣2,y1)、B(﹣1,y2)、C(2,y3),则( )