题目内容
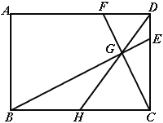
【题目】如图，在矩形ABCD中，点H为边BC的中点，点G为线段DH上一点，且∠BGC=90°，延长BG交CD于点E，延长CG交AD于点F，当CD=4，DE=1时，则DF的长为（ ）
A.2B.
C.
D.
【答案】A
【解析】
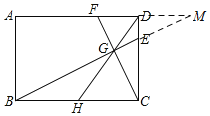
延长AD，BE相交于点M，可得△DFG∽△HCG，△DMG∽△HBG，根据相似三角形的性质可得DF=DM，由△MDE∽△CDF可得
，进而得出
，再根据比例的性质解答即可．
解：如图，延长AD，BE相交于点M，
∵DF∥CH，
∴△DFG∽△HCG，
∴ 
，
∵DM∥BH，
∴△DMG∽△HBG，
∴ 
，
∵CH=BH， ∴DF=DM，
又∵矩形
△MDE∽△CDF，
∴ 
∴ 
∴
∴DF＝
．
故选：A．
练习册系列答案
中考解读考点精练系列答案
相关题目
