题目内容
 如图,AE⊥AB,∠ABC=90°,AC平分∠BAD,∠3=∠4,则下列结论中错误的是
如图,AE⊥AB,∠ABC=90°,AC平分∠BAD,∠3=∠4,则下列结论中错误的是
- A.BC∥AE
- B.∠1+∠7=∠5+∠6
- C.∠APE=90°-
 ∠7
∠7 - D.∠6=∠8
D
分析:此题利用排除法,根据条件可证出∠EAB+∠ABC=180°,可得BC∥AE;再根据内角与外角的关系可以证出∠2+∠7=∠5+∠6,进而得到∠1+∠7=∠5+∠6;再利用角平分线性质可以求出∠APB=90°+ ∠7,即可得到∠APE=90°-
∠7,即可得到∠APE=90°- ∠7,从而可以选出答案.
∠7,从而可以选出答案.
解答: 解;∵AE⊥AB,
解;∵AE⊥AB,
∴∠EAB=90°,
∵∠ABC=90°,
∴∠EAB+∠ABC=180°,
∴BC∥AE,故A正确;
∵AC平分∠BAD,
∴∠1=∠2,
∵∠2+∠7=∠9,
∠5+∠6=∠9,
∴∠2+∠7=∠5+∠6,
∴∠1+∠7=∠5+∠6,
故B正确;
∵∠1+∠2+∠3+∠4+∠7=180°,
∴(∠1+∠2+∠3+∠4)=180°-∠7,
∵∠1=∠2,∠3=∠4,
∴∠1+∠3=90°- ∠7
∠7
∴∠APB=180°-(∠1+∠3)=90°+ ∠7,
∠7,
∴∠APE=180°-(90°+ ∠7)=90°-
∠7)=90°- ∠7,
∠7,
故C正确;
∵A、B、C都正确,
∴只有D错误.
故选D.
点评:此题主要考查了角平分线的性质,三角形外角与内角的关系,平行线的判定,题目综合性较强,但是难度不大,较好.
分析:此题利用排除法,根据条件可证出∠EAB+∠ABC=180°,可得BC∥AE;再根据内角与外角的关系可以证出∠2+∠7=∠5+∠6,进而得到∠1+∠7=∠5+∠6;再利用角平分线性质可以求出∠APB=90°+
 ∠7,即可得到∠APE=90°-
∠7,即可得到∠APE=90°- ∠7,从而可以选出答案.
∠7,从而可以选出答案.解答:
 解;∵AE⊥AB,
解;∵AE⊥AB,∴∠EAB=90°,
∵∠ABC=90°,
∴∠EAB+∠ABC=180°,
∴BC∥AE,故A正确;
∵AC平分∠BAD,
∴∠1=∠2,
∵∠2+∠7=∠9,
∠5+∠6=∠9,
∴∠2+∠7=∠5+∠6,
∴∠1+∠7=∠5+∠6,
故B正确;
∵∠1+∠2+∠3+∠4+∠7=180°,
∴(∠1+∠2+∠3+∠4)=180°-∠7,
∵∠1=∠2,∠3=∠4,
∴∠1+∠3=90°-
 ∠7
∠7∴∠APB=180°-(∠1+∠3)=90°+
 ∠7,
∠7,∴∠APE=180°-(90°+
 ∠7)=90°-
∠7)=90°- ∠7,
∠7,故C正确;
∵A、B、C都正确,
∴只有D错误.
故选D.
点评:此题主要考查了角平分线的性质,三角形外角与内角的关系,平行线的判定,题目综合性较强,但是难度不大,较好.

练习册系列答案
相关题目
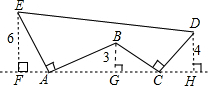 如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )
如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )| A、50 | B、62 | C、65 | D、68 |
 如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是
如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是 如图,AE⊥AB,AD⊥AC,AB=AE,∠B=∠E,求证:BD=CE.
如图,AE⊥AB,AD⊥AC,AB=AE,∠B=∠E,求证:BD=CE. 如图,AE⊥AB,AD⊥AC,AB=AE,∠B=∠E,求证:
如图,AE⊥AB,AD⊥AC,AB=AE,∠B=∠E,求证: 如图,AE⊥AB,∠ABC=90°,AC平分∠BAD,∠3=∠4,则下列结论中错误的是( )
如图,AE⊥AB,∠ABC=90°,AC平分∠BAD,∠3=∠4,则下列结论中错误的是( )