题目内容
 如图,AE⊥AB,AD⊥AC,AB=AE,∠B=∠E,求证:BD=CE.
如图,AE⊥AB,AD⊥AC,AB=AE,∠B=∠E,求证:BD=CE.
分析:通过条件可证得∠CAE=∠DAB,已知AB=AE,∠B=∠E,可得到△DAB≌△CAE(ASA),即可得到BD=CE.
解答:证明:∵AE⊥AB,AD⊥AC,
∴∠EAB=∠DAC=90°,
∴∠EAB+∠EAD=∠DAC+∠EAD,
∴∠CAE=∠DAB;
∴在△DAB与△CAE中
,
∴△DAB≌△CAE,
∴BD=CE.
∴∠EAB=∠DAC=90°,
∴∠EAB+∠EAD=∠DAC+∠EAD,
∴∠CAE=∠DAB;
∴在△DAB与△CAE中
|
∴△DAB≌△CAE,
∴BD=CE.
点评:三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.本题图形看似复杂,找准全等的三角形是解决本题的关键.

练习册系列答案
相关题目
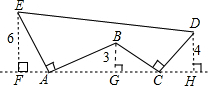 如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )
如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )| A、50 | B、62 | C、65 | D、68 |
 如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是
如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是 如图,AE⊥AB,AD⊥AC,AB=AE,∠B=∠E,求证:
如图,AE⊥AB,AD⊥AC,AB=AE,∠B=∠E,求证: 如图,AE⊥AB,∠ABC=90°,AC平分∠BAD,∠3=∠4,则下列结论中错误的是( )
如图,AE⊥AB,∠ABC=90°,AC平分∠BAD,∠3=∠4,则下列结论中错误的是( )