题目内容
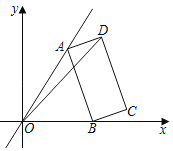
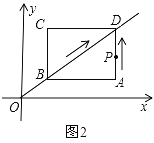
【题目】如图,![]() ,矩形
,矩形![]() 的边
的边![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上,![]() ,
,![]() ,矩形
,矩形![]() 沿射线
沿射线![]() 方向,以每秒1个单位长度的速度运动.同时点
方向,以每秒1个单位长度的速度运动.同时点![]() 从点
从点![]() 出发沿折线
出发沿折线![]() 以每秒1个单位长度的速度向终点
以每秒1个单位长度的速度向终点![]() 运动,当点
运动,当点![]() 到达点
到达点![]() 时,矩形
时,矩形![]() 也停止运动,设点
也停止运动,设点![]() 的运动时间为
的运动时间为![]() ,
,![]() 的面积为
的面积为![]() .
.
(1)分别写出点![]() 到
到![]() 、
、![]() 的距离(用含
的距离(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 不与矩形
不与矩形![]() 的顶点重合时,求
的顶点重合时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)设点![]() 到
到![]() 的距离为
的距离为![]() ,当
,当![]() 时,求
时,求![]() 的值;
的值;
(4)若在点![]() 出发的同时,点
出发的同时,点![]() 从点
从点![]() 以每秒
以每秒![]() 个单位长度的速度向终点A运动,当点
个单位长度的速度向终点A运动,当点![]() 停止运动时,点
停止运动时,点![]() 与矩形
与矩形![]() 也停止运动,设点
也停止运动,设点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,当
,当![]() 的一边与
的一边与![]() 的一边平行时,直接写出线段
的一边平行时,直接写出线段![]() 的长.
的长.
【答案】(1)![]() ,
,![]() ;(2)当0<t<3时,
;(2)当0<t<3时,![]() ;当3<t<7时,
;当3<t<7时,![]() ;(3)
;(3)![]() ;(4)
;(4)![]() ,
,![]() ,
,![]()
【解析】
(1)过点B作x轴垂线,利用相似三角形可求得;
(2)分2种情况,一种是点P在AD上,另一种是点P在CD上,然后利用三角形面积公式可求得;
(3)直接令![]() 即可求出;
即可求出;
(4)存在3种情况,第一种是:QP∥BD,第二种是EP∥CD或EQ∥CB,第三种是QE∥BD,分别按照几何性质分析求解.
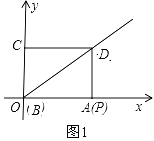
(1)如下图,过点B作x轴垂线,垂足为点M
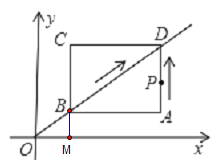
根据平移的特点,可得∠BOM=∠DBA
∵∠BMO=∠DAB=90°,∴△BMO∽△DAB
∵AB=4,AD=BC=3
∴BD=5
∵![]() ,OB=t
,OB=t
∴BM=![]() ,OM=
,OM=![]()
(2)情况一:当0<t<3时,图形如下,过点P作OD的垂线,交OD于点N
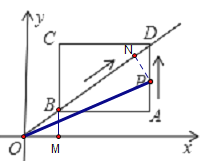
∵∠NDP=∠BDA,∠PND=∠BAD,∴△PND∽△BAD
∵AP=t,∴PD=3-t
∵![]() ,∴PN=
,∴PN=![]()
图中,OD=5+t
∴![]()
情况二:当3<t<7时,图形如下,过点P作OD的垂线,交OD于点N
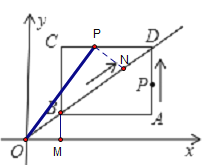
图中,PD=t-3,OD=5+t
同理,△PND∽△BCD,可得PN=![]()
∴![]()
(3)情况一:当0<t<3时
则h=PN=![]()
∵![]()
∴![]()
解得:t=![]()
情况二:当3<t<7时
则h=PN=![]()
∵![]()
∴![]()
解得:t=7(舍)
(4)情况一:QP∥BD,图形如下
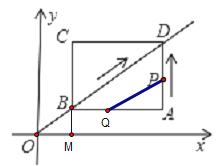
由题意可得:BQ=![]() ,AP=t,则QA=4-
,AP=t,则QA=4-![]() ,DP=3-t
,DP=3-t
∵BD∥QP
∴![]()
代入得:4![]()
解得:t=![]()
∴OD=5+t=![]()
情况二:如下图,EP∥CD(或EQ∥CB)
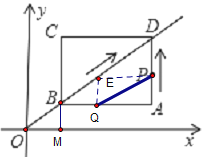
∵点E是点A关于QP对称的点
∴EP=PA,EQ=QA,QP=QP
∴△APQ≌△EPQ
∵EP∥CD,CD⊥AD
∴EP⊥AD
∴∠APQ=∠EPQ=45°
∴△AQP是等腰直角三角形,AQ=PA
∴4-![]()
解得:t=![]()
∴OD=5+t=![]()
情况三:如下图,QE∥BD,延长QE交DA于点N

∵△APQ≌△EPQ,∴∠QEP=∠QAP=90°
∴△ENP是等腰直角三角形
∵QN∥BD,∴∠NQA=∠DBA,∠A=∠A
∴△QNA∽△BDA
∵BQ=![]() ,AP=t,QA=4-
,AP=t,QA=4-![]() ,DP=3-t
,DP=3-t
∴![]()
∴QN=5-![]() ,NA=3-t
,NA=3-t
∴EN=QN-QE=QN-QA=1-![]() ,NP=NA-AP=3-2t,EP=PA=t
,NP=NA-AP=3-2t,EP=PA=t
∴在Rt△ENP中,![]()
解得:t=![]() 或t=3(舍)
或t=3(舍)
∴OD=5+t=![]()