ЬтФПФкШн
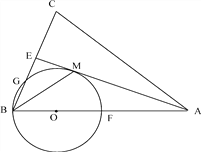
ЁОЬтФПЁПШчЭМЃЌдкЕШБпЁїABCжаЃЌ ![]() ЃЎЖЏЕуPДгЕуBГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуAдЫЖЏЃЛЭЌЪБЖЏЕуQДгЕуAГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуCдЫЖЏЃЎзїPMЁЭBCгкЕуMЃЌСЌНсPQЃЎвдPMЁЂPQЮЊСкБпзїЁѕPMNQЃЌЩшЁѕPMNQгыЁїABCжиЕўВПЗжЭМаЮЕФУцЛ§ЮЊSЃЌЕуQЕФдЫЖЏЪБМфЮЊtУыЃЎ
ЃЎЖЏЕуPДгЕуBГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуAдЫЖЏЃЛЭЌЪБЖЏЕуQДгЕуAГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуCдЫЖЏЃЎзїPMЁЭBCгкЕуMЃЌСЌНсPQЃЎвдPMЁЂPQЮЊСкБпзїЁѕPMNQЃЌЩшЁѕPMNQгыЁїABCжиЕўВПЗжЭМаЮЕФУцЛ§ЮЊSЃЌЕуQЕФдЫЖЏЪБМфЮЊtУыЃЎ
ЃЈ1ЃЉ![]() _____________ЃЈгУКЌtЕФДњЪ§ЪНБэЪОЃЉЃЎ
_____________ЃЈгУКЌtЕФДњЪ§ЪНБэЪОЃЉЃЎ
ЃЈ2ЃЉЕБЫФБпаЮPMNQЪЧСтаЮЪБЃЌЧѓtЕФжЕЃЎ
ЃЈ3ЃЉЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ1ЃЛЃЈ3ЃЉ
ЃЛЃЈ2ЃЉ1ЃЛЃЈ3ЃЉ
ЁОНтЮіЁП
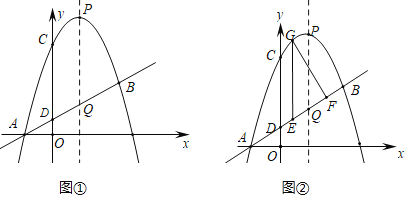
ЃЈ1ЃЉИљОн30ЖШЕФжБНЧШ§НЧаЮЕФаджЪПЩЕУPMЕФГЄЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌзїИЈжњЯпЃЌЙЙНЈжБНЧШ§НЧаЮЃЌИљОнЙДЙЩЖЈРэКЭ30ЁуЕФжБНЧШ§НЧаЮЕФаджЪЕУЃКAGКЭPGЕФГЄЃЌИљОнAB=4ЃЌСаЗНГЬПЩЕУtЕФжЕЃЛ
ЃЈ3ЃЉЗжШ§жжЧщПіЃКЂй0ЁмtЃМ![]() ЪБЃЌШчЭМ3ЃЌбгГЄQNНЛBCгкGЃЌЁѕPMNQгыЁїABCжиЕўВПЗжЭМаЮЪЧЁѕPMNQЃЛ
ЪБЃЌШчЭМ3ЃЌбгГЄQNНЛBCгкGЃЌЁѕPMNQгыЁїABCжиЕўВПЗжЭМаЮЪЧЁѕPMNQЃЛ
ЂкЕБ![]() ЁмtЃМ2ЪБЃЌШчЭМ4ЃЌЁѕPMNQгыЁїABCжиЕўВПЗжЭМаЮЪЧЬнаЮPMGQЃЛ
ЁмtЃМ2ЪБЃЌШчЭМ4ЃЌЁѕPMNQгыЁїABCжиЕўВПЗжЭМаЮЪЧЬнаЮPMGQЃЛ
ЂлЕБ2ЁмtЁм4ЪБЃЌШчЭМ5ЃЌPгыAжиКЯЃЌЁѕPMNQгыЁїABCжиЕўВПЗжЭМаЮЪЧЬнаЮPMGQЃЌИљОнУцЛ§ЙЋЪНПЩЕУНсТлЃЎ
НтЃКЃЈ1ЃЉЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯB=60ЁуЃЌ
ЁпPMЁЭBCЃЌ
ЁрЁЯPMB=90ЁуЃЌ
ЁпPB=2tЃЌ
ЁрPM=![]() ЃЛ
ЃЛ
ЙЪД№АИЮЊЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЫФБпаЮPMNQЪЧСтаЮЃЌ

Й§QзїQGЁЭABгкGЃЌ
гЩЬтвтЕУЃКAQ=tЃЌPB=2tЃЌ
ЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯA=ЁЯB=60ЁуЃЌ
ЁрЁЯAQG=30ЁуЃЌ
ЁрAG=![]() ЃЌGQ=
ЃЌGQ=![]() ЃЌ
ЃЌ
RtЁїBPMжаЃЌЁЯBMP=90ЁуЃЌ
ЁрЁЯBPM=30ЁуЃЌ
ЁрPM=![]() ЃЌ
ЃЌ
ЁпЫФБпаЮPMNQЪЧСтаЮЃЌ
ЁрPQ=PM=![]() ЃЌ
ЃЌ
ЁрPG=![]() ЃЌ
ЃЌ
ЁрAB=AG+PG+PBЃЌМД2t+![]() +
+![]() =4ЃЌ
=4ЃЌ
Ёрt=1ЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕБNдкBCЩЯЪБЃЌЫФБпаЮPMNQЪЧОиаЮЃЌ

ЁрPQЁЮBCЃЌ
ЁрЁЯAPQ=ЁЯB=60ЁуЃЌЁЯAQP=ЁЯC=60ЁуЃЌ
ЁрЁїAPQЪЧЕШБпШ§НЧаЮЃЌ
ЁрAP=AQ=tЃЌ
ЁрAB+PB=4ЃЌМДt+2t=4ЃЌ
Ёрt=![]() ЃЛ
ЃЛ
ЗжШ§жжЧщПіЃК
Ђй0ЁмtЃМ![]() ЪБЃЌШчЭМЃЌбгГЄQNНЛBCгкGЃЌPMNQгыЁїABCжиЕўВПЗжЭМаЮЪЧЁѕPMNQЃЌ
ЪБЃЌШчЭМЃЌбгГЄQNНЛBCгкGЃЌPMNQгыЁїABCжиЕўВПЗжЭМаЮЪЧЁѕPMNQЃЌ

ЁпPMЁЮQNЃЌPMЁЭBCЃЌ
ЁрQGЁЭBCЃЌ
RtЁїCQGжаЃЌЁЯCQG=30ЁуЃЌCQ=4-tЃЌ
ЁрGQ=![]() ЃЈ4-tЃЉЃЌCG=
ЃЈ4-tЃЉЃЌCG=![]() CQ=
CQ=![]() ЃЈ4-tЃЉЃЌ
ЃЈ4-tЃЉЃЌ
ЁрMG=![]() ЃЌ
ЃЌ
ЁрS=SPMNQ=PMMG=![]() ЃЛ
ЃЛ
ЂкЕБ![]() ЁмtЃМ2ЪБЃЌШчЭМЃЌPMNQгыЁїABCжиЕўВПЗжЭМаЮЪЧЬнаЮPMGQЃЌ
ЁмtЃМ2ЪБЃЌШчЭМЃЌPMNQгыЁїABCжиЕўВПЗжЭМаЮЪЧЬнаЮPMGQЃЌ

ЁрS=![]() MG(QG+PM)=
MG(QG+PM)=![]() ЃЛ
ЃЛ
ЂлЕБ2ЁмtЁм4ЪБЃЌШчЭМЃЌPгыAжиКЯЃЌPMNQгыЁїABCжиЕўВПЗжЭМаЮЪЧЬнаЮPMGQЃЌ

BM=2ЃЌPM=![]() ЃЌCG=
ЃЌCG=![]() ЃЌ
ЃЌ
ЁрMG=![]() =
=![]() ЃЌ
ЃЌ
ЁрS=![]() MG(QG+PM)=
MG(QG+PM)=![]() ЃЛ
ЃЛ
Ёр .
.

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИЁОЬтФПЁПЖўДЮКЏЪ§![]() (aЃЌbЃЌcЮЊГЃЪ§ЃЌЧвaЁй0)жаЕФxгыyЕФВПЗжЖдгІжЕШчЯТБэЃК
(aЃЌbЃЌcЮЊГЃЪ§ЃЌЧвaЁй0)жаЕФxгыyЕФВПЗжЖдгІжЕШчЯТБэЃК
x | Ё | -1 | 0 | 1 | 3 | Ё |
y | Ё | -3 | 1 | 3 | 1 | Ё |
дђЯТСаХаЖЯжае§ШЗЕФЪЧЃЈ ЃЉ
A.ХзЮяЯпПЊПкЯђЩЯB.ХзЮяЯпгыyжсНЛгкИКАыжс
C.ХзЮяЯпЕФЖЅЕуЮЊ(1ЃЌ3)D.вЛдЊЖўДЮЗНГЬax2+bx+c=0ЕФе§Иљдк3гы4жЎМф