题目内容
点P在图形M上, 点Q在图形N上,记 为线段PQ长度的最大值,
为线段PQ长度的最大值, 为线段PQ长度的最小值,图形M,N的平均距离
为线段PQ长度的最小值,图形M,N的平均距离 .
.
(1)在平面直角坐标系 中,⊙O是以O为圆心,2的半径的圆,且A
中,⊙O是以O为圆心,2的半径的圆,且A ,B
,B ,求
,求 及
及 ;(直接写出答案即可)
;(直接写出答案即可)
(2)半径为1的⊙C的圆心C与坐标原点O重合,直线 与
与 轴交于点D,与
轴交于点D,与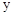 轴交于点F,记线段DF为图形G,求
轴交于点F,记线段DF为图形G,求 ;
;
(3)在(2)的条件下,如果⊙C的圆心C从原点沿 轴向右移动,⊙C的半径不变,且
轴向右移动,⊙C的半径不变,且 ,求圆心C的横坐标.
,求圆心C的横坐标.
 为线段PQ长度的最大值,
为线段PQ长度的最大值, 为线段PQ长度的最小值,图形M,N的平均距离
为线段PQ长度的最小值,图形M,N的平均距离 .
.(1)在平面直角坐标系
 中,⊙O是以O为圆心,2的半径的圆,且A
中,⊙O是以O为圆心,2的半径的圆,且A ,B
,B ,求
,求 及
及 ;(直接写出答案即可)
;(直接写出答案即可)(2)半径为1的⊙C的圆心C与坐标原点O重合,直线
 与
与 轴交于点D,与
轴交于点D,与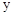 轴交于点F,记线段DF为图形G,求
轴交于点F,记线段DF为图形G,求 ;
;(3)在(2)的条件下,如果⊙C的圆心C从原点沿
 轴向右移动,⊙C的半径不变,且
轴向右移动,⊙C的半径不变,且 ,求圆心C的横坐标.
,求圆心C的横坐标.(1)2,4;(2)3;(3) 或
或 .
.
 或
或 .
.试题分析:(1)作出图形,根据定义求解;(2)如图,过点O作OH⊥DF于点H,交圆C于点M,圆C与x轴的左交点为点N,根据点到直线上一点的距离的最小值为该点到垂足的距离可知,
 ,从而应用直线上点的坐标与方程的关系和锐角三角函数(或相似三角形)知识求出OH,进而求出MH,又
,从而应用直线上点的坐标与方程的关系和锐角三角函数(或相似三角形)知识求出OH,进而求出MH,又 ,因此根据定义可求
,因此根据定义可求 ;(3)分
;(3)分 ,
, ,
, ,
, 四种情况讨论即可.
四种情况讨论即可.试题解析:(1)如图,根据勾股定理可求:OA=1,OB=4,
∴
 .
.∴
 ,
,  .
.
(2)如图,过点O作OH⊥DF于点H,交圆C于点M,圆C与x轴的左交点为点N,则
根据点到直线上一点的距离的最小值为该点到垂足的距离可知,
 ,
,∵直线
 与
与 轴交于点D,与
轴交于点D,与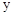 轴交于点F,∴D(4,0),F(0,
轴交于点F,∴D(4,0),F(0, ),即OD=4,OF=
),即OD=4,OF= .
.∴
 .∴
.∴ .∴
.∴ .∴
.∴ .
.又
 ,∴
,∴ .
.
(3)设点C的横坐标为x(x≥0),
当
 时,线段与圆无公共点,圆心离点D最远,
时,线段与圆无公共点,圆心离点D最远, ,解得:
,解得: .
.当
 时,线段与圆无公共点,圆心离点F最远,
时,线段与圆无公共点,圆心离点F最远, ,解得:
,解得: (不符合
(不符合 ,舍去).
,舍去).当
 时,线段与圆有公共点,
时,线段与圆有公共点, ,解得:
,解得: (舍去负值).
(舍去负值).当
 时,
时, ,不符合题意舍去.
,不符合题意舍去.综上所述,点C的横坐标为
 或
或 .
.
练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目



