题目内容
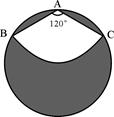
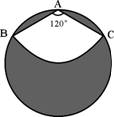
如图,有一直径是1米的圆形铁皮,要从中剪出一个圆心角是120°的扇形ABC,求:
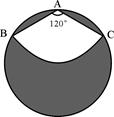
(1)被剪掉阴影部分的面积。
(2)若用所留的扇形铁皮围成一个圆锥,该圆锥底面圆的半径是多少?
(1)
(2)解析:
解:(1)设O为圆心,连OA、OB …………(1')

∵OA=OC=OB AB=AC
∴△ABO≌△ACO (sss) 又∠BAC=120°
∴∠BAO=∠CAO=60°
∴△ABO是等边三角形
∴AB=
 … ………………………………………(3')
… ………………………………………(3')∴S扇形ABC=
 π(
π( )
)=
 …………………………………(5')
…………………………………(5')∴S阴影=π (
 )2-
)2-
=
 …………………………………(6')
…………………………………(6')(2)在扇形ABC中,
 的长为
的长为 ·
· =
= …………………(7')
…………………(7')设底面圆的半径为r。
则 2πr=
 ………………………………………………(8')
………………………………………………(8')∴r=
 … ……………………………………………(9')
… ……………………………………………(9') 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
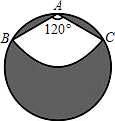 如图,有一直径是1米的圆形铁皮,要从中剪出一个圆心角是120°的扇形ABC,
如图,有一直径是1米的圆形铁皮,要从中剪出一个圆心角是120°的扇形ABC,