Question

如图所示，A、B两地之间有一条河，原来从A地到B地需要经过DC，沿折线A→D→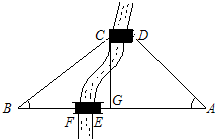C→B到达，现在新建了桥EF，可直接沿直线AB从A地到达B地．已知BC=10km，∠A=45°，∠B=37°，桥DC和AB平行．
（1）求两桥之间的距离CG（CG⊥AB）；
（2）从A地到达B地可比原来少走多少路程？（精确到0.1km）．
（参考数据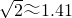：，sin37°≈0.60，cos37°≈0.80）

Answer 1

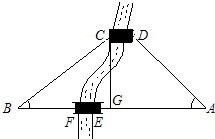解：（1）∵CG⊥AB于G，
∴∠BGC=90°．
在△BGC中，∠BGC=90°，∠B=37°，BC=10km，
∴CG=BC•sin37°≈10×0.60≈6.0（km）．
故两桥之间的距离CG约为6.0km；

（2）如图，过点D作DH⊥AB于H，DM∥CB交AB于M．
∵DC∥AB，
∴四边形DCBM为平行四边形．
∴DC=MB，MD=BC=10km．
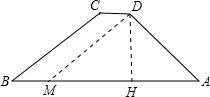∴两条路线路程之差为：AD+CD+BC-AB=AD+DM-AM．
在Rt△DMH中，DH=CG≈6.0km，
MH=DM•cos37°≈10×0.80≈8.0km．
在Rt△ADH中，
AD=DH≈1.41×6.0≈8.46km．
AH=DH≈6.0km．
∴AD+DM-AM≈（8.46+10）-（6.0+8.0）≈4.46≈4.5（km）．
即从A地到B地可比原来少走约4.5km．
分析：（1）在RT△BGC中，由sin∠B=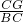，即可求出CG的长度；
（2）从A地到达B地比原来少走的路程就是（AD+CD+BC-AB）的长．过点D作DH⊥AB于H，DG∥CB交AB于G．将梯形问题转化为三角形中求解．
点评：本题考查了解直角三角形的实际应用，将梯形中的问题转化为三角形问题是解决梯形问题的常用方法，常作的辅助线有平移一腰、平移对角线、作高等．