题目内容
如图,在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧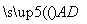 上取一点E使∠EBC = ∠DEC,延长BE依次交AC于G,交⊙O于H.
上取一点E使∠EBC = ∠DEC,延长BE依次交AC于G,交⊙O于H.
(1)求∠AGB的度数;
(2)若∠ABC= 45°,⊙O的直径等于17,BD =15,求CE的长.
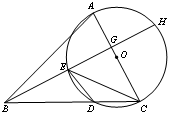
证明:(1)连结AD
∵∠DAC = ∠DEC ∠EBC = ∠DEC
∴∠DAC = ∠EBC
又∵AC是⊙O的直径 ∴∠ADC=90°
∴∠DCA+∠DAC=90° ∴∠EBC+∠DCA = 90°
∴∠BGC=180°–(∠EBC+∠DCA) = 180°–90°=90°
∴∠AGB=90°
(2)∵∠BDA=180°–∠ADC = 90° ∠ABC = 45° ∴∠BAD = 45°
∴BD = AD
∵BD =15 ∴AD =15
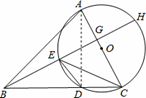 又∵∠ADC = 90° AC =17
又∵∠ADC = 90° AC =17
∴由勾股定理 DC= 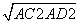 =8
=8
∴BC=BD+DC=8+15=23
∵∠EBC=∠DEC,∠BCE=∠ECD,
∴△BCE∽△ECD
∴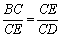
∴CE=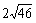

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案我市某中学九年级学生对市民“创建精神文明城市“知晓率采取随机抽样的方法进行问卷调查,问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不太了解“、“从未听说”五个等级,统计后的数据整理如下表:
| 等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 | 从未听说 |
| 频数 | 40 | 60 | 48 | 36 | 16 |
| 频率 | 0.2 | m | 0.24 | 0.18 | 0.08 |
(1)本次问卷调查抽取的样本容量为 ,表中m的值为 ;
(2)根据表中的数据计算等级为“非常广解”的频数在扇形统计图中所对应扇形的圆心角的度数;
(3)根据上述统计结果,请你对政府相关部门提出一句话建议.

 >0)过A(-3,y1)、B(-7,,y2) 、C(4,y3)三点,把y1 、y2 、y3从小到大的顺序排列为
>0)过A(-3,y1)、B(-7,,y2) 、C(4,y3)三点,把y1 、y2 、y3从小到大的顺序排列为  的解集是
的解集是 ,则( )
,则( )  ≤
≤ B.
B. C.
C. D.
D.
 三点可以确定一个圆时,
三点可以确定一个圆时, 需要满足的条件 .
需要满足的条件 . 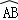 的中点,CD与AB的交点为E,则
的中点,CD与AB的交点为E,则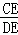 等于( )
等于( )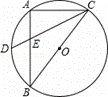
 的自变量
的自变量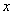 的取值范围是( )
的取值范围是( )  D.
D.
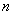 个小球,其中两个是白球,其余为红球,这些球的形状、大小、质地等完全相同,从袋中随机地取出一个球,它是红球的概率是
个小球,其中两个是白球,其余为红球,这些球的形状、大小、质地等完全相同,从袋中随机地取出一个球,它是红球的概率是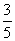 .
. ,随机地取出一个小球后不放回,再随机地取出一个小球,请用画树状图或列表的方法求第二次取出小球标号大于第一次取出小球标号的概率.
,随机地取出一个小球后不放回,再随机地取出一个小球,请用画树状图或列表的方法求第二次取出小球标号大于第一次取出小球标号的概率.