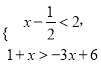题目内容
【题目】已知关于![]() 的方程组
的方程组![]() ,
,
(1)若用代入法求解,可由①得:![]() = ③,把③代入②解得
= ③,把③代入②解得![]() = ,将其代入③解得
= ,将其代入③解得![]() = ,∴原方程组的解为 ;
= ,∴原方程组的解为 ;
(2)若此方程组的解![]() 互为相反数,求这个方程组的解及
互为相反数,求这个方程组的解及![]() 的值.
的值.
【答案】(1)![]() ;
;![]() ;
;![]() ;
; ;(2)
;(2)![]() ;
;![]()
【解析】试题分析:(1)观察方程组中未知数的系数可得①中x的系数为1,可将①转化为用含y的式子表示x得③,然后把③代入另一个方程②中,消去x,得到关于y的一元一次方程,解之得y的值,再将y的值代入③即可求出x的值,最后用大括号的形式写出原方程组的解;
(2)根据方程组的解互为相反数可得x=-y,代入方程①求出y,进而求出x,再代入方程②求出m即可.
试题解析:
解:(1)若用代入法求解,可由①得![]() ,
,
把③代入②解得![]() ,
,
将其代入③解得![]() ,
,
∴原方程组的解为 .
.
故答案为:![]() ;
;![]() ;
;![]() ;
; ;
;
(2)解:∵方程组的解![]() 互为相反数,
互为相反数,
∴![]() ,
,
将③代入①得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴方程组的解是![]() ,
,![]() .
.

练习册系列答案
相关题目