题目内容
 (2006•福州质检)七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,如图是一副七巧板,若已知其中一块平行四边形PHQD的面积是8,请根据你对七巧板制作过程的认识,求动点A沿A→B→E→F→H→P→D所走过的所有路线的长.
(2006•福州质检)七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,如图是一副七巧板,若已知其中一块平行四边形PHQD的面积是8,请根据你对七巧板制作过程的认识,求动点A沿A→B→E→F→H→P→D所走过的所有路线的长.分析:根据图,以及七巧板的性质,可知EFHO是正方形;PHQD是平行四边形;由正方形的性质可知:△ABO≌△ADO;△BEF≌△HOP;由此可得BE=EF=EO=FH=PD;PH=DQ=
CD;再设正方形的边长为a,将各边长依次求出即可解答.
| 1 |
| 2 |
解答:解:由七巧板制作过程可知,E、F、H、P、Q、O分别是BO、BC、FQ、OD、CD和BD的中点,EFHO是正方形;PHQD是平行四边形;由正方形的性质可知:△ABO≌△ADO;△BEF≌△HOP;由此可得BE=EF=EO=FH=PD;PH=DQ=
CD;
A→B→E→H→P→D所走过的所有路线的长是:
AB+BE+EF+FH+HP+PD
=AB+BE+EO+OP+HP+PD
=AB+BD+
CD
=
AB+BD
设正方形ABCD边长为a,得BD=
AB=
a
SPHQD=QD•PD•sin∠PDQ=
CD•
BD•sin45°
又∵
a•
•
=
a2=8
∴a=8
∴点所走过的路线长为12+8
.
| 1 |
| 2 |
A→B→E→H→P→D所走过的所有路线的长是:
AB+BE+EF+FH+HP+PD
=AB+BE+EO+OP+HP+PD
=AB+BD+
| 1 |
| 2 |
=
| 3 |
| 2 |
设正方形ABCD边长为a,得BD=
| 2 |
| 2 |
SPHQD=QD•PD•sin∠PDQ=
| 1 |
| 2 |
| 1 |
| 4 |
又∵
| 1 |
| 2 |
| ||
| 4 |
| ||
| 2 |
| 1 |
| 8 |
∴a=8
∴点所走过的路线长为12+8
| 2 |
点评:本题借助七巧板考查了正方形、等腰直角三角形的性质,以及勾股定理等知识,熟练掌握上述知识点是解答本题的关键.

练习册系列答案
相关题目
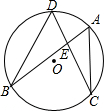 (2006•福州质检)如图,⊙O中弦AB、CD相交于点E,连接BD、AC,则图中相等的角共有( )对.
(2006•福州质检)如图,⊙O中弦AB、CD相交于点E,连接BD、AC,则图中相等的角共有( )对. (2006•福州质检)将一副三角尺按如图的位置摆放,则∠BOC的度数是
(2006•福州质检)将一副三角尺按如图的位置摆放,则∠BOC的度数是