题目内容
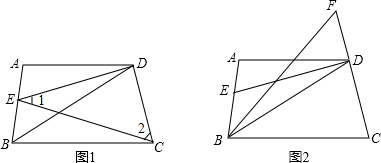
如图1,四边形ABCD中,AD∥BC,DE平分∠ADB,∠BDC=∠BCD.
(1)求证:∠1+∠2=90°.
(2)如图2,若∠ABD的平分线与CD的延长经交于点F,且∠F=60°,求∠ABC的度数.
(1)求证:∠1+∠2=90°.
(2)如图2,若∠ABD的平分线与CD的延长经交于点F,且∠F=60°,求∠ABC的度数.

考点:平行线的性质,三角形内角和定理
专题:
分析:(1)由AD∥BC,DE平分∠ADB,得∠ADC+∠BCD=180,∠BDC=∠BCD,得出∠1+∠2=90°;
(2)由DE平分∠ADB,CD平分∠ABD,四边形ABCD中,AD∥BC,∠F=60°,得出∠ABC=∠ABD+∠DBC=∠ABD+∠ADB,即∠ABC=60°.
(2)由DE平分∠ADB,CD平分∠ABD,四边形ABCD中,AD∥BC,∠F=60°,得出∠ABC=∠ABD+∠DBC=∠ABD+∠ADB,即∠ABC=60°.
解答:(1)证明:AD∥BC,
∠ADC+∠BCD=180,
∵DE平分∠ADB,
∠BDC=∠BCD,
∴∠ADE=∠EDB,
∠BDC=∠BCD,
∵∠ADC+∠BCD=180°,
∴∠EDB+∠BDC=90°,
∴∠1+∠2=90°.
(2)解:∵∠FBD+∠BDE=90°-∠F=30°,DE平分∠ADB,BF平分∠ABD,
∴∠ADB+∠ABD=2(∠FBD+∠BDE)=60°,
又∵四边形ABCD中,AD∥BC,
∴∠DBC=∠ADB,
∴∠ABC=∠ABD+∠DBC=∠ABD+∠ADB,即∠ABC=60°;
∠ADC+∠BCD=180,
∵DE平分∠ADB,
∠BDC=∠BCD,
∴∠ADE=∠EDB,
∠BDC=∠BCD,
∵∠ADC+∠BCD=180°,
∴∠EDB+∠BDC=90°,
∴∠1+∠2=90°.
(2)解:∵∠FBD+∠BDE=90°-∠F=30°,DE平分∠ADB,BF平分∠ABD,
∴∠ADB+∠ABD=2(∠FBD+∠BDE)=60°,
又∵四边形ABCD中,AD∥BC,
∴∠DBC=∠ADB,
∴∠ABC=∠ABD+∠DBC=∠ABD+∠ADB,即∠ABC=60°;
点评:本题考查的是平行线的性质、角平分线的性质,解决问题的关键在于熟悉掌握知识要点,并且善于运用角与角之间的联系进行传递.

练习册系列答案
相关题目
下列各算式正确的是( )
| A、sin30°+sin30°=sin60° | ||
| B、tan60°-tan30°=tan30° | ||
| C、cos(60°-30°)=cos60°-cos30° | ||
D、3tan30°=
|
下列一元二次方程中,无实数根的方程是( )
| A、x2+2=0 |
| B、x2-x-2=0 |
| C、x2+x-2=0 |
| D、x2+x=0 |
下列各式中用科学记数法表示正确的是( )
| A、0.05=5×10-3 |
| B、0.0034=34×10-3 |
| C、-0.00012=1.2×10-4 |
| D、2.12=2.12×100 |
若两数之和为负数,则两数之积一定( )
| A、正数 | B、零 |
| C、负数 | D、以上答案都有可能 |
 请把+(-3),(-2)2,-|-2.5|,0,-(-1.5)这五个数先化简,再将化简结果按从小到大顺序,从左到右串个糖葫芦,把数填在“○”内.
请把+(-3),(-2)2,-|-2.5|,0,-(-1.5)这五个数先化简,再将化简结果按从小到大顺序,从左到右串个糖葫芦,把数填在“○”内.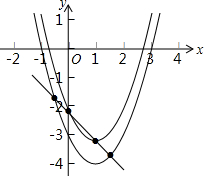 如图,抛物线c1:y=(x-1)2-
如图,抛物线c1:y=(x-1)2-