题目内容
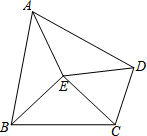已知四边形ABCD内一点E，若EA=EB=EC=ED，∠BAD=70°，则∠BCD的度数为________．
110°
分析：先由EA=EB=EC=ED，得出A、B、C、D四点共圆，再根据圆内接四边形的对角互补得出∠BCD=180°-∠BAD．
解答：∵点E为四边形ABCD内一点，且EA=EB=EC=ED，
∴A、B、C、D四点共圆，
∴∠BCD=180°-∠BAD=180°-70°=110°．
故答案为110°．
点评：本题考查了四点共圆的条件及圆内接四边形的性质，由已知判断出A、B、C、D四点共圆是解题的关键．
分析：先由EA=EB=EC=ED，得出A、B、C、D四点共圆，再根据圆内接四边形的对角互补得出∠BCD=180°-∠BAD．
解答：∵点E为四边形ABCD内一点，且EA=EB=EC=ED，
∴A、B、C、D四点共圆，
∴∠BCD=180°-∠BAD=180°-70°=110°．
故答案为110°．
点评：本题考查了四点共圆的条件及圆内接四边形的性质，由已知判断出A、B、C、D四点共圆是解题的关键．
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
如图，已知四边形ABCD内接于直径为3的圆O，对角线AC是直径，对角线AC和BD的交点是P，AB=BD，且PC=0.6，求四边形ABCD的周长．
的延长线分别交于点F、E，且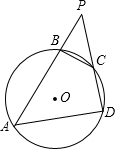
已知四边形ABCD内接于⊙O，分别延长AB和DC相交于点P，