题目内容
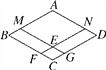
如图,四边形ABCD是平行四边形,点M,N分别在AB,AD上,且AM=AN,BM=DN,MG∥AD,NF∥AB,点F,G分别在BC,CD上,MG与NF相交于点E,则图中的菱形共有________个.
练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
题目内容
如图,四边形ABCD是平行四边形,点M,N分别在AB,AD上,且AM=AN,BM=DN,MG∥AD,NF∥AB,点F,G分别在BC,CD上,MG与NF相交于点E,则图中的菱形共有________个.

 高中必刷题系列答案
高中必刷题系列答案