Question

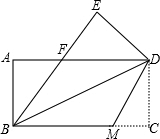
如图，把一张矩形的纸片ABCD沿对角线BD折叠，使点C落在点E处，BE与AD交于点F．
（1）线段BF与DF相等吗？请说明理由．
（2）若将折叠的图形恢复原状，点F与BC边上的点G正好重合，连接DG，试判断四边形BGDF的形状，并说明理由．
（3）若AB=4，AD=7，在（1）、（2）的条件下，求线段DG的长．

Answer 1

分析：（1）根据平行线的性质和折叠不变性求出两角相等，再判断出两边相等；
（2）判断出四边形BGDF是平行四边形，再根据BG=BF，得出四边形BGDF是菱形．
（3）设AF=x，则BF=FD=7-x，利用勾股定理即可求出DF的长，即为DG的长．

解答：解：（1）BF=DF．
∵FD∥BC，
∴∠FDB=∠CBD，
由折叠不变性知，∠FBD=∠GBD，
∴∠FBD=∠FDB，
∴FB=FD；

（2）∵FD=FB，BG=BF，
∴FD=BG，
又∵FD∥BG，
∴四边形BGDF是平行四边形，
∵BG=BF，
∴四边形BGDF是菱形；

（3）设AF=x，则BF=FD=7-x．
在Rt△ABF中，
x²+4²=（7-x）²，
解得，x=

33

14

．
则DF=7-

33

14

=4

9

14

．
即DG=4

9

14

．

点评：此题结合矩形的性质、菱形的判定和性质，考查了翻折不变性，综合性较强，是一道好题．