题目内容
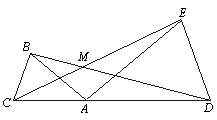
已知:点C、A、D在同一条直线上,∠ABC=∠ADE=α,线段 BD、CE交于点M.
(1)如图1,若AB=AC,AD=AE
①问线段BD与CE有怎样的数量关系?并说明理由;
②求∠BMC的大小(用α表示);
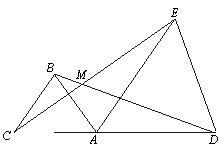
(2)如图2,若AB= BC=kAC,AD =ED=kAE
则线段BD与CE的数量关系为 ,∠BMC= (用α表示);
(3)在(2)的条件下,把△ABC绕点A逆时针旋转180°,在备用图中作出旋转后的图形(要求:尺规作图,不写作法,保留作图痕迹),连接 EC并延长交BD于点M.
 则∠BMC= (用α表示).
则∠BMC= (用α表示).
 | |||
 | |||
|
| ||||
解:
(1) ①BD=CE …………1′
∵AD=AE
 ∴∠AED=∠ADE=α
∴∠AED=∠ADE=α
∴∠DAE=180°-2∠ADE=180°-2α
同理可得:∠BAC=180°-2α
∴∠DAE =∠BAC
∴∠DAE+∠BAE =∠BAC+∠BAE
即:∠BAD =∠CAE …………2′
|
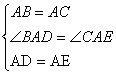
∴△ABD≌△ACE(SAS)
∴BD=CE …………………………4′
② ∵△ABD≌△ACE
∴∠BDA =∠CEA
∵
|
∴∠BMC=∠MCD+∠CEA
=∠EAD=180°-2α…………………………6′
 (2)BD=kCE ……………………7′
(2)BD=kCE ……………………7′
![]() ……………………8′
……………………8′
(3)画图正确…………………10′
![]() …………………12′
…………………12′
|

练习册系列答案
相关题目




