题目内容
7.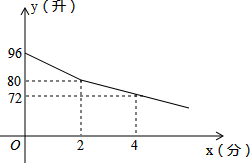 某校部分住校生,放学后到学校锅炉房打水,每人接水2L,他们同时打开两个放水龙头,后来因故障关闭一个放水龙头,假设前后两人接水间隔时间忽略不计,且不发生泼洒,锅炉内的余水量y(L)与接水时间x(min)的函数图象如图.
某校部分住校生,放学后到学校锅炉房打水,每人接水2L,他们同时打开两个放水龙头,后来因故障关闭一个放水龙头,假设前后两人接水间隔时间忽略不计,且不发生泼洒,锅炉内的余水量y(L)与接水时间x(min)的函数图象如图.(1)求出炉内的余水量y(L)与接水时间x(min)的函数关系式;
(2)前15名同学接水结束共需要多久;
(3)小敏说:“今天我们寝室的8位同学去锅炉房连续接完水恰好用了3(min).”试判断,他的说法是否可能,说明理由.
分析 (1)设炉内的余水量y(L)与接水时间x(min)的函数关系式为y=kx+b(k≠0),分0≤x≤2和x≥2两种情况,根据点的坐标利用待定系数法,即可求出炉内的余水量y(L)与接水时间x(min)的函数关系式;
(2)先求出15名同学接完水后锅炉内的剩余水量,再利用一次函数图象上点的坐标特征即可求出此时的x值,此题得解;
(3)假设小敏的说法成立,设在0≤x≤2中,小敏寝室接到水的同学有a个,则在x≥2中,小敏寝室接到水的同学有(8-a)个,根据8名同学接完水共用3分钟,可得出关于a的一元一次方程,解之即可得出a、8-a和$\frac{2}{8}$a的值,由a和8-a均为正整数且$\frac{2}{8}$a=1<2,即可得出小敏的说法可能成立.
解答 解:(1)设炉内的余水量y(L)与接水时间x(min)的函数关系式为y=kx+b(k≠0),
当0≤x≤2时,将点(0,96)、(2,80)代入y=kx+b,
得:$\left\{\begin{array}{l}{b=96}\\{2k+b=80}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-8}\\{b=96}\end{array}\right.$,
∴y=-8x+96(0≤x≤2);
当x≥2时,将点(2,80)、(4,72)代入y=kx+b,
得:$\left\{\begin{array}{l}{2k+b=80}\\{4k+b=72}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-4}\\{b=88}\end{array}\right.$,
∴y=-4x+88(x≥2).
∴炉内的余水量y(L)与接水时间x(min)的函数关系式为y=$\left\{\begin{array}{l}{-8x+96(0≤x≤2)}\\{-4x+88(x≥2)}\end{array}\right.$.
(2)15名同学接水总量为15×2=30(升),
锅炉内剩余水量为96-30=66(升),
当y=-4x+88=66时,x=$\frac{11}{2}$=5.5,
∴前15名同学接水结束共需要5.5分钟.
(3)假设小敏的说法成立,设在0≤x≤2中,小敏寝室接到水的同学有a个,则在x≥2中,小敏寝室接到水的同学有(8-a)个,
根据题意得:$\frac{2}{8}$a+$\frac{2}{4}$(8-a)=3,
解得:a=4,
∴8-a=4.
∵a和8-a均为正整数,且$\frac{2}{8}$a=1<2,
∴小敏的说法可能成立.
点评 本题考查了一次函数的应用、待定系数法求一次函数解析式、一次函数图象上点的坐标特征以及一元一次方程的应用,解题的关键是:(1)分0≤x≤2和x≥2两种情况,根据点的坐标利用待定系数法求出函数关系式;(2)利用一次函数图象上点的坐标求出前15名同学接水结束共需时间;(3)找准等量关系,找出关于a的一元一次方程.

 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案| A. | a2×a3=a6 | B. | (a+b)2=a2+b2 | C. | (-a2)3=-a6 | D. | a2+a3=a5 |
| A. | 调查札幌亚冬会女子越野滑雪1.4公里决赛参赛运动员兴奋剂的使用情况 | |
| B. | 调查中国民众对美国在韩部署萨德系统持反对态度的比例 | |
| C. | 调查中国国产航母各零部件的质量 | |
| D. | 调查某班学生对感动中国2016年度人物我校高2004级校友秦珇飞的知晓率 |





 如图,正五边形ABCDE内接于⊙O,若⊙O的半径为5,则弧AB的长为2π.
如图,正五边形ABCDE内接于⊙O,若⊙O的半径为5,则弧AB的长为2π.
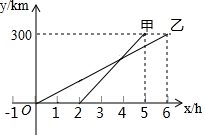 甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,乙出发2h后甲再出发,且甲、乙两人离A地的距离y甲、y乙与时间x之间的函数图象如图所示.
甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,乙出发2h后甲再出发,且甲、乙两人离A地的距离y甲、y乙与时间x之间的函数图象如图所示.