题目内容
3.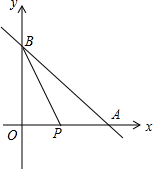 如图,直线y=kx+b分别交x轴、y轴正半轴于点A、B,其中A(6,0),P为x轴正半轴上一个动点.
如图,直线y=kx+b分别交x轴、y轴正半轴于点A、B,其中A(6,0),P为x轴正半轴上一个动点.(1)若OB:OA=4:3,求点B坐标及一次函数解析式;
(2)在(1)的条件下,连结BP,若BP平分∠OBA,求点P坐标及△BPA的面积;
(3)若OB=OA,在第一象限内作等腰直角△BPM,其中∠BPM=90°,直线MA交y轴于点C,则点C是否为定点?请说明理由.
分析 (1)先确定出OB,进而得出点B的坐标,再用待定系数法确定出直线解析式;
(2)根据角平分线定理得出方程求解即可得出点P坐标,最后用三角形的面积公式求解即可;
(3)先判断出△OBP≌△NPM,得出MN=OP=m,PN=OB=6,即可得出点M的坐标,最后用待定系数法得出直线AM解析式,即可得出点C坐标,即可判断.
解答 解(1)∵A(6,0),
∴OA=6,
∵OB:OA=4:3,
∴OB=8,
∴B(0,8),
∴$\left\{\begin{array}{l}{6k+b=0}\\{b=8}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=8}\end{array}\right.$,
∴一次函数解析式为y=-$\frac{4}{3}$x+8,
(2)∵OA=6,OB=8,
∴AB=10,
设P(a,0),
∴OP=a,ap=6-a,
∵BP平分∠OBA,
∴$\frac{OB}{AB}=\frac{OP}{AP}$,
∴$\frac{8}{10}=\frac{a}{6-a}$,
∴a=$\frac{8}{3}$,
∴P($\frac{8}{3}$,0),PA=6-$\frac{8}{3}$=$\frac{10}{3}$,
∴S△BPA=$\frac{1}{2}$PA×OB=$\frac{1}{2}$×$\frac{10}{3}$×8=$\frac{40}{3}$,
(3)点C是定点,理由:如图,
由(1)知,OA=6,
∵OB=OA,
∴OB=6,
∴B(0,6),
过点M作MN⊥OA,
设P(m,0),
由旋转知,BP=MP,∠BPM=90°,
∴∠BPO+∠MPN=90°,
∵∠OBP+∠BPO=90°,
∴∠OBP=∠NPM,
在△OBP和△NPM中,$\left\{\begin{array}{l}{∠OBP=∠NPM}\\{∠BOP=∠PNM}\\{PB=PM}\end{array}\right.$,
∴△OBP≌△NPM,
∴MN=OP=m,PN=OB=6,
∴ON=m+6,
∴M(m+6,m),
∵A(6,0),
∴直线AM的解析式为y=x-6,
∴C(0,-6)为定点.
点评 此题是一次函数综合题,主要考查了待定系数法,三角形的面积公式,全等三角形的判定,解本题的关键是判断出△OBP≌△NPM,是一道难度不大的中考常考题.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案 有理数a、b在数轴上的位置如图所示,则下列结论正确的是( )
有理数a、b在数轴上的位置如图所示,则下列结论正确的是( )| A. | $\frac{a}{b}>0$ | B. | a-b>0 | C. | ab>0 | D. | a+b<0 |
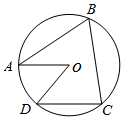 如图,A、B、C、D四个点均在⊙O上,∠AOD=50°,AO∥DC,则∠B的度数为( )
如图,A、B、C、D四个点均在⊙O上,∠AOD=50°,AO∥DC,则∠B的度数为( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
| A. | (2,-3) | B. | (-2,3) | C. | (-2,-3 ) | D. | (3,2) |