Question

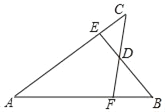
【题目】如图，已知正方形ABCD的边长为4，点E、F分别在边AB，BC上，且AE=BF=1，CE，DF交于点O，下面结论：（1）∠DOC=90°；（2）OC=OE ；（3）S△ODC=S四边形BEOF.

其中正确的有____________（只填写序号）

Answer 1

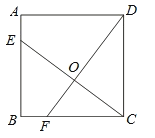
【答案】（1）（3）

【解析】

由正方形ABCD的边长为4，AE=BF=1，利用SAS易证得△EBC≌△FCD，然后全等三角形的对应角相等，易证得（1）∠DOC=90°正确；（2）由线段垂直平分线的性质与正方形的性质，可得（2）错误；由（1）易证得（3）正确．

∵正方形ABCD的边长为4，

∴BC=CD=4,∠B=∠DCF=90°，

∵AE=BF=1，

∴BE=CF=41=3，

在△EBC和△FCD中,，

∴△EBC≌△FCD(SAS),

∴∠CFD=∠BEC，

∴∠BCE+∠BEC=∠BCE+∠CFD=90°，

∴∠DOC=90°；

故（1）正确；

连接DE，如图所示：

若OC=OE，

∵DF⊥EC，

∴CD=DE，

∵CD=AD<DE(矛盾)，

故（2）错误；

∵△EBC≌△FCD，

∴S△EBC=S△FCD，

∴S△EBCS△FOC=S△FCDS△FOC，

即S△ODC=S四边形BEOF.

故（3）正确；

故答案为：（1）（3）.