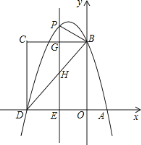
题目内容
【题目】在平面直角坐标系![]() 中,二次函数
中,二次函数![]() 的图象与
的图象与![]() 轴正半轴交于
轴正半轴交于![]() 点.
点.
![]() 求证:该二次函数的图象与
求证:该二次函数的图象与![]() 轴必有两个交点;
轴必有两个交点;
![]() 设该二次函数的图象与
设该二次函数的图象与![]() 轴的两个交点中右侧的交点为点
轴的两个交点中右侧的交点为点![]() ,若
,若![]() ,将直线
,将直线![]() 向下平移
向下平移![]() 个单位得到直线
个单位得到直线![]() ,求直线
,求直线![]() 的解析式;
的解析式;
![]() 在
在![]() 的条件下,设
的条件下,设![]() 为二次函数图象上的一个动点,当
为二次函数图象上的一个动点,当![]() 时,点
时,点![]() 关于
关于![]() 轴的对称点都在直线
轴的对称点都在直线![]() 的下方,求
的下方,求![]() 的取值范围.
的取值范围.
【答案】![]() 解析;
解析;![]() 直线
直线![]() ;
;![]()
![]() 的取值范围为:
的取值范围为:![]() .
.
【解析】
(1)直接利用根的判别式,结合完全平方公式求出△的符号进而得出答案;
(2)首先求出B,A点坐标,进而求出直线AB的解析式,再利用平移规律得出答案;
(3)根据当-3<p<0时,点M关于x轴的对称点都在直线l的下方,当p=0时,q=1;当p=-3时,q=12m+4;结合图象可知:-(12m+4)≤2,即可得出m的取值范围.
![]() 令
令![]() ,则
,则
![]() ,
,
∵二次函数图象与![]() 轴正半轴交于
轴正半轴交于![]() 点,
点,
∴![]() ,且
,且![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴该二次函数的图象与轴必有两个交点;
![]() 令
令![]() ,
,
解得:![]() ,
,![]() ,
,
由![]() 得
得![]() ,故
,故![]() 的坐标为
的坐标为![]() ,
,
又因为![]() ,
,
所以![]() ,即
,即![]() ,
,
则可求得直线![]() 的解析式为:
的解析式为:![]() .
.
再向下平移![]() 个单位可得到直线
个单位可得到直线![]() ;
;
![]() 由
由![]() 得二次函数的解析式为:
得二次函数的解析式为:![]() .
.
∵![]() 为二次函数图象上的一个动点,
为二次函数图象上的一个动点,
∴![]() .
.
∴点![]() 关于轴的对称点
关于轴的对称点![]() 的坐标为
的坐标为![]() .
.
∴![]() 点在二次函数
点在二次函数![]() 上.
上.
∵当![]() 时,点
时,点![]() 关于
关于![]() 轴的对称点都在直线
轴的对称点都在直线![]() 的下方,
的下方,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
结合图象可知:![]() ,
,
解得:![]() .
.
∴![]() 的取值范围为:
的取值范围为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目