题目内容
如图,矩形ABCD在平面直角坐标系![]() 中,BC边在x轴上,点A(-1,2),点C(3,0) .动点P从点A出发,以每秒1个单位的速度沿AD向点D运动,到达点D后停止.把BP的中点M绕点P逆时针旋转90°到点N,连接PN,DN.设P的运动时间为t秒.
中,BC边在x轴上,点A(-1,2),点C(3,0) .动点P从点A出发,以每秒1个单位的速度沿AD向点D运动,到达点D后停止.把BP的中点M绕点P逆时针旋转90°到点N,连接PN,DN.设P的运动时间为t秒.
1.经过1秒后,求出点N的坐标;
2.当t为何值时,△PND的面积最大?并求出这个最大值
3.求在整个过程中,点N运动的路程是多少?
1.当t=1时,AP=1,过点N作NQ⊥AD于点Q,易证△BAP∽△PQN
所以![]() ∴PQ=1,NQ=
∴PQ=1,NQ=![]() ∴N(1,
∴N(1, ![]() )……………2分
)……………2分
2.当点P运动时间为t秒时
NQ=![]() ,PD=4-t
,PD=4-t
∴y=![]()
![]() …………………4分
…………………4分
当t=2时,y最大………………6分
y最大=2………7分
3.因为PQ=1,AP=t
所以N(t,2-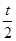 )
)
当t=0时,2-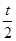 =2;当t=4时,2-
=2;当t=4时,2-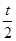 =0并且点D沿直线y=2-
=0并且点D沿直线y=2-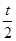 运动,
运动,
所以:点N运动的路程是![]() …………………10分
…………………10分
解析:(1)利用△BAP∽△PQN求出N点的坐标;
(2)先列出△PND的面积方程,然后通过二次的性质进行求解;
(3)分段求出N的路程,然后求它们之和

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
 (2013•太原)如图,矩形ABCD在第一象限,AB在x轴正半轴上,AB=3,BC=1,直线y=
(2013•太原)如图,矩形ABCD在第一象限,AB在x轴正半轴上,AB=3,BC=1,直线y=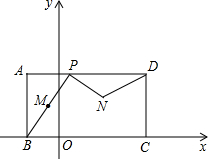 BP的中点M绕点P逆时针旋转90°到点N,连接PN,DN.设P的运动时间为t秒.
BP的中点M绕点P逆时针旋转90°到点N,连接PN,DN.设P的运动时间为t秒.
 如图,矩形ABCD在第一象限,AB在x轴正半轴上,AB=3,BC=1,直线y=
如图,矩形ABCD在第一象限,AB在x轴正半轴上,AB=3,BC=1,直线y= x-1经过点C交x轴于点E,双曲线y=
x-1经过点C交x轴于点E,双曲线y= 经过点D,则k的值为 .
经过点D,则k的值为 . 经过点C交x轴于点E,双曲线
经过点C交x轴于点E,双曲线 经过点D,则k的值为 .
经过点D,则k的值为 .