题目内容
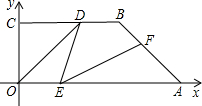
 如图,OA是⊙O的半径,弦BC垂直平分OA,垂直为E点,则
如图,OA是⊙O的半径,弦BC垂直平分OA,垂直为E点,则 的度数是
的度数是
- A.60°
- B.90°
- C.120°
- D.150°
C
分析:先根据垂径定理求出OE= OB,再解直角三角形即可.
OB,再解直角三角形即可.
解答: 解:连接OB,OC,
解:连接OB,OC,
∵OA⊥BC,由垂径定理知,点E是BC的中点
∵点E是OA的中点,∴OE= OB
OB
∴cos∠BOE= =
=
∴∠BOE=60°
∴∠BOC=120°
由弧的度数与它所对的圆心角相等知, 的度数是120°.
的度数是120°.
故选C.
点评:本题利用了垂径定理,余弦的概念,弧的度数与它所对的圆心角相等求解.
分析:先根据垂径定理求出OE=
 OB,再解直角三角形即可.
OB,再解直角三角形即可.解答:
 解:连接OB,OC,
解:连接OB,OC,∵OA⊥BC,由垂径定理知,点E是BC的中点
∵点E是OA的中点,∴OE=
 OB
OB∴cos∠BOE=
 =
=
∴∠BOE=60°
∴∠BOC=120°
由弧的度数与它所对的圆心角相等知,
 的度数是120°.
的度数是120°.故选C.
点评:本题利用了垂径定理,余弦的概念,弧的度数与它所对的圆心角相等求解.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目

 上的点E处.
上的点E处. 如图,直角梯形OABC的直角顶点是坐标原点,边OA,OC分别在X轴,y轴的正半轴上.OA∥BC,D是BC上一点,BD=
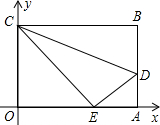
如图,直角梯形OABC的直角顶点是坐标原点,边OA,OC分别在X轴,y轴的正半轴上.OA∥BC,D是BC上一点,BD= 如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.
如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.