题目内容
【题目】在矩形ABCD中,AD=3,CD=4,点E在CD上,且DE=1.
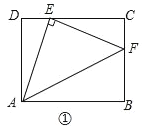
(1)感知:如图①,连接AE,过点E作EF丄AE,交BC于点F,连接AE,易证:△ADE≌△ECF(不需要证明);
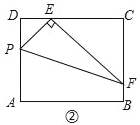
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE和△ECF相似;
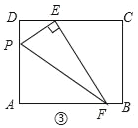
(3)应用:如图③,若EF交AB于点F,EF丄PE,其他条件不变,且△PEF的面积是6,则AP的长为_____.
【答案】3﹣![]()
【解析】试题分析:感知:先利用矩形性质得:∠D=∠C=90°,再利用同角的余角相等得:∠DAE=∠FEC,根据已知边的长度计算出AD=CE=3,则由ASA证得:△ADE≌△ECF;
探究:利用两角相等证明△PDE∽△ECF;
应用:作辅助线,构建如图②一样的相似三角形,利用探究得:△PDE∽△EGF,则 ![]() =
=![]() ,所以
,所以 ![]() =
=![]() ,再利用△PEF的面积是6,列式可得:PEEF=12,两式结合可求得PE的长,利用勾股定理求PD,从而得出AP的长.
,再利用△PEF的面积是6,列式可得:PEEF=12,两式结合可求得PE的长,利用勾股定理求PD,从而得出AP的长.
试题解析:证明:感知:如图①.∵四边形ABCD为矩形,∴∠D=∠C=90°,∴∠DAE+∠DEA=90°.∵EF⊥AE,∴∠AEF=90°,∴∠DEA+∠FEC=90°,∴∠DAE=∠FEC.∵DE=1,CD=4,∴CE=3.∵AD=3,∴AD=CE,∴△ADE≌△ECF(ASA);
探究:如图②.∵四边形ABCD为矩形,∴∠D=∠C=90°,∴∠DPE+∠DEP=90°.∵EF⊥PE,∴∠PEF=90°,∴∠DEP+∠FEC=90°,∴∠DPE=∠FEC,∴△PDE∽△ECF;
应用:如图③,过F作FG⊥DC于G.∵四边形ABCD为矩形,∴AB∥CD,∴FG=BC=3.∵PE⊥EF,∴S△PEF=![]() PEEF=6,∴PEEF=12,同理得:△PDE∽△EGF,∴
PEEF=6,∴PEEF=12,同理得:△PDE∽△EGF,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴EF=3PE,∴3PE2=12,∴PE=±2.∵PE>0,∴PE=2.在Rt△PDE中,由勾股定理得:PD=
,∴EF=3PE,∴3PE2=12,∴PE=±2.∵PE>0,∴PE=2.在Rt△PDE中,由勾股定理得:PD=![]() =
=![]() ,∴AP=AD﹣PD=3﹣
,∴AP=AD﹣PD=3﹣![]() .故答案为:3﹣
.故答案为:3﹣![]() .
.


【题目】![]() 朗读者
朗读者![]() 自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级
自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级![]() 、
、![]() 班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩
班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩![]() 满分为100分
满分为100分![]() 如图所示.
如图所示.
平均数 | 中位数 | 众数 | |
九 | 85 | 85 | |
九 | 80 |
![]() 根据图示填写表格;
根据图示填写表格;
![]() 结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
![]() 如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.

【题目】从2开始,连续的偶数相加,它们和的情况如下表:
加数的个数n | S |
1 | 2=1×2 |
2 | 2+4=6=2×3 |
3 | 2+4+6=12=3×4 |
4 | 2+4+6+8=20=4×5 |
5 | 2+4+6+8+10=30=5×6 |
(1)若n=8时,则S的值为_____________.
(2)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+8+…+2n=__________________.
(3)根据上题的规律计算2+4+6+8+10+…+98+100![]() 的值.
的值.