题目内容
如图，在矩形ABCD中，AB=9，AD=3| 3 |
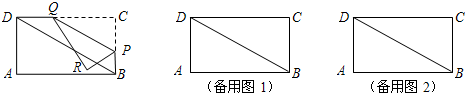
（1）求∠CPQ的度数；
（2）当x取何值时，点R落在矩形ABCD的AB边上？
（3）求y与x之间的函数关系式；
（4）①当x取何值时，重叠部分的面积最大，并求出这个最大值；②当x取何值时，重叠部分的面积等于矩形面积的
| 7 |
| 27 |
分析：（1）根据矩形的性质推出AB=CD，AD=BC，根据解直角三角形求出∠CDB=30°，根据平行线的性质和数据线的内角和定理求出即可；
（2）根据轴对称的性质可知△RPQ≌△CPQ，推出∠RPQ=∠CPQ，RP=CP，在△RPB中得出2（3
-x）=x，求出即可；
（3）当点R在矩形ABCD的内部或AB边上时，求出S△CPQ的值，推出当0＜x≤2
时，y=
x2，当R在矩形ABCD的外部，求出PF=2BP=2（3
-x），求出RF\ER=
x-6，进一步求出S△ERF即可；
（4）①当0＜x≤2
时，求出y的最大值，当2
＜x＜3
时，求出在x=
时，y最大值=9
，②矩形面积=9×3
=27
，根据计算求出当0＜x＜2
时，y的值不可能是矩形面积的
；当2
＜x＜3
时，根据题意得出方程-
x2+18x-18
=7
，求出方程的解即可．
（2）根据轴对称的性质可知△RPQ≌△CPQ，推出∠RPQ=∠CPQ，RP=CP，在△RPB中得出2（3
| 3 |
（3）当点R在矩形ABCD的内部或AB边上时，求出S△CPQ的值，推出当0＜x≤2
| 3 |
| ||
| 2 |
| 3 |
| 3 |
（4）①当0＜x≤2
| 3 |
| 3 |
| 3 |
| 18 | ||
2
|
| 3 |
| 3 |
| 3 |
| 3 |
| 7 |
| 27 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
解答：解：（1）∵四边形ABCD是矩形，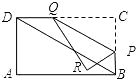
∴AB=CD，AD=BC，
∵AB=9，AD=3
，∠C=90°，
∴CD=9，BC=3
，
∴tan∠CDB=
=
，∴∠CDB=30°，
∵PQ∥BD，
∴∠CQP=∠CDB=30°，
∴∠CPQ=90°-∠CQP=60°，
答：∠CPQ的度数是60°．
（2）解：如图1，由轴对称的性质可知，△RPQ≌△CPQ，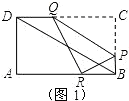
∴∠RPQ=∠CPQ，RP=CP，
由（1）知：∠CQP=30°，∴∠RPQ=∠CPQ=60°，
∴∠RPB=60°，
∴RP=2BP，
∵CP=x，
∴PR=x，PB=3
-x，
在△RPB中，根据题意得：2（3
-x）=x，
解这个方程得：x=2
，
答：当x取2
时，点R落在矩形ABCD的AB边上．
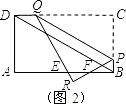
（3）解：当点R在矩形ABCD的内部或AB边上时，
如图1：FE的范围是0＜x≤2
，
S△CPQ=
×CP×CQ=
x×
x=
x2，
∵△RPQ≌△CPQ，
∴当0＜x≤2
时，y=
x2，
当R在矩形ABCD的外部时（如图2），2
＜x＜3
，
在Rt△PFB中，∵∠RPB=60°，
∴PF=2BP=2（3
-x），
∵RP=CP=x，
∴RF=RP-PF=3x-6
，
在Rt△ERF中，
∵∠EFR=∠PFB=30°，
∴ER=
x-6，
∴S△ERF=
×ER×FR=
x2-18x+18
，
∵y=S△RPQ-S△ERF，
∴当2
＜x＜3
时，y=-
x2+18x-18
，
答：y与x之间的函数解析式是：y=
．
（4）解：①当0＜x≤2
时，函数y=
x2随自变量的增大而增大，
∴y的最大值是6
，
当2
＜x＜3
时，y=-
x2+18x-18
=7
，
∵-
＜0，
∴在x=
=3
时，y的最大值=
=9
，
∴当2
＜x＜3
时，y没有最大值．
②矩形面积=9×3
=27
，
当0＜x≤2
时，y的最大值是6
，
而矩形面积的
的值=
×27
=7
，
而7
＞6
，
∴当0＜x＜2
时，y的值不可能是矩形面积的
；
当2
＜x＜3
时，根据题意，得：-
x2+18x-18
=7
，
解这个方程，得x=3
±
，
∵3
+
＞3
，
∴x=3
+
不合题意，舍去，
∴x=3
-
，
答：当x=3
-
时，△PQR与矩形ABCD重叠部分的面积等于矩形面积的
．
∴AB=CD，AD=BC，
∵AB=9，AD=3
| 3 |
∴CD=9，BC=3
| 3 |
∴tan∠CDB=
| BC |
| CD |
| ||
| 3 |
∵PQ∥BD，
∴∠CQP=∠CDB=30°，
∴∠CPQ=90°-∠CQP=60°，
答：∠CPQ的度数是60°．
（2）解：如图1，由轴对称的性质可知，△RPQ≌△CPQ，
∴∠RPQ=∠CPQ，RP=CP，
由（1）知：∠CQP=30°，∴∠RPQ=∠CPQ=60°，
∴∠RPB=60°，
∴RP=2BP，
∵CP=x，
∴PR=x，PB=3
| 3 |
在△RPB中，根据题意得：2（3
| 3 |
解这个方程得：x=2
| 3 |
答：当x取2
| 3 |
（3）解：当点R在矩形ABCD的内部或AB边上时，
如图1：FE的范围是0＜x≤2
| 3 |
S△CPQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
∵△RPQ≌△CPQ，
∴当0＜x≤2
| 3 |
| ||
| 2 |
当R在矩形ABCD的外部时（如图2），2
| 3 |
| 3 |
在Rt△PFB中，∵∠RPB=60°，
∴PF=2BP=2（3
| 3 |
∵RP=CP=x，
∴RF=RP-PF=3x-6
| 3 |
在Rt△ERF中，
∵∠EFR=∠PFB=30°，
∴ER=
| 3 |
∴S△ERF=
| 1 |
| 2 |
3
| ||
| 2 |
| 3 |
∵y=S△RPQ-S△ERF，
∴当2
| 3 |
| 3 |
| 3 |
| 3 |
答：y与x之间的函数解析式是：y=
|
（4）解：①当0＜x≤2
| 3 |
| ||
| 2 |
∴y的最大值是6
| 3 |
当2
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
∵-
| 3 |
∴在x=
| 18 | ||
2
|
| 3 |
4
| ||||
-4
|
| 3 |
∴当2
| 3 |
| 3 |
②矩形面积=9×3
| 3 |
| 3 |
当0＜x≤2
| 3 |
| 3 |
而矩形面积的
| 7 |
| 27 |
| 7 |
| 27 |
| 3 |
| 3 |
而7
| 3 |
| 3 |
∴当0＜x＜2
| 3 |
| 7 |
| 27 |
当2
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
解这个方程，得x=3
| 3 |
| 2 |
∵3
| 3 |
| 2 |
| 3 |
∴x=3
| 3 |
| 2 |
∴x=3
| 3 |
| 2 |
答：当x=3
| 3 |
| 2 |
| 7 |
| 27 |
点评：本题主要考查对矩形的性质，全等三角形的性质和判定，三角形的面积，三角形的内角和定理，解一元二次方程，翻折变换，二次函数的最值等知识点的理解和掌握，综合运用这些性质进行计算是解此题的关键．
练习册系列答案
相关题目
如图，在矩形ABCD中，AB=4cm，BC=8cm，点P从点A出发以1cm/s的速度向点B运动，点Q从点B出发以2cm/s的速度向点C运动，设经过的时间为xs，△PBQ的面积为ycm2，则下列图象能反映y与x之间的函数关系的是（ ）
．
动过程中，Q点停留了1s，图②是P、Q两点在折线AB-BC-CD上相距的路程S（cm）与时间t（s）之间的函数关系图象．
如图，在矩形ABCD中，对角线AC，BD相交于点O，∠AOB=60°，AB=6，则AD=（ ）
DE，EF与AB交于点F，设CE=x，BF=y．