题目内容
如图,P是⊙O的直径AB延长线上一点,点C在⊙O上,AC=PC,∠ACP=120°.

(1)求证:CP是⊙O的切线;
(2)若AB=4cm,求图中阴影部分的面积.
【答案】
(1)证明见解析;(2)阴影部分的面积=2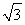 ﹣
﹣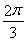 .
.
【解析】
试题分析:(1)根据等腰三角形中等边对等角即可求得∠OCP的度数,即可证得;
(2)利用扇形的面积公式,以及阴影部分的面积=S△OCP﹣S扇形OCB即可求解.
试题解析:(1)连接OC.
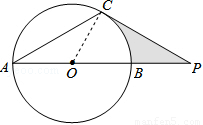
∵∠ACP=120°,AC=PC,
∴∠A=∠P=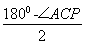 =30°,
=30°,
∴∠COP=2∠A=60°,
在△OCP中,∠OCP=180°﹣60°﹣30°=90°.
∴OC⊥CP,
∴CP是⊙O的切线;
(2)AB=4cm,
则OC=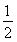 AB=2cm,
AB=2cm,
∵直角△OCP中,∠P=30°,
∴OP=2OC=4,
∴CP=2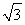 ,
,
∴S△OCP=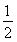 OC•CP=
OC•CP=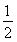 ×2×2
×2×2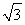 =2
=2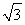 (cm2),
(cm2),
S扇形OCB=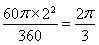 (cm2),
(cm2),
则阴影部分的面积=2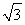 ﹣
﹣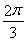 (cm2).
(cm2).
考点:切线的判定.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 22、已知,如图AB是⊙O的直径,BC是⊙O的弦,⊙O的割线PDE垂直于AB于点F,交BC于点G,∠A=∠BCP.
22、已知,如图AB是⊙O的直径,BC是⊙O的弦,⊙O的割线PDE垂直于AB于点F,交BC于点G,∠A=∠BCP. 如图,是⊙O的直径AB=8,△ABC为正三角形,则图中阴影部分的面积之和为( )
如图,是⊙O的直径AB=8,△ABC为正三角形,则图中阴影部分的面积之和为( ) (2013•南昌)如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.
(2013•南昌)如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图. (2013•北京)如图AB是⊙O的直径,PA,PC与⊙O分别相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E.
(2013•北京)如图AB是⊙O的直径,PA,PC与⊙O分别相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E. 如图AB是⊙O的直径,弧BC度数是60,D是劣弧BC的中点,P是AB上的动点,若⊙O的半径为1,则PC+PD的最小值是
如图AB是⊙O的直径,弧BC度数是60,D是劣弧BC的中点,P是AB上的动点,若⊙O的半径为1,则PC+PD的最小值是