Question

如图，是⊙O的直径AB=8，△ABC为正三角形，则图中阴影部分的面积之和为（　　）

• A．

  3

• B．2
• C．3

  3

• D．4

  3

Answer 1

分析：连接AE、BD，则可判断AD=BE=

1

2

AB，点D是AC中点，点E是BC中点，阴影部分的面积等于等边三角形DEC的面积，从而计算出答案．

解答：解：连接AE，BD，

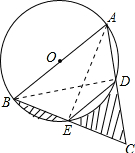
∵AB是直径，
∴∠ADB=90°，
又∵△ABC为正三角形，
∴∠BAD=60°，
∴∠ABD=30°，
∴AD=

1

2

AB=

1

2

AC=4，点D是AC中点，
同理可得BE=

1

2

AB=

1

2

BC=4，点E是BC中点，
∴DE是△ABC的中位线，
∴△DEC为等边三角形，
∴DE=EC=BE=4，
则阴影部分的面积等于等边三角形DEC的面积，
即阴影部分的面积=S_△EDC=

3

4

×4²=4

3

．
故选D．

点评：本题考查了扇形的面积的计算，证明△EDC是等边三角形，边长是4，理解而

BE

和弦BE围成的部分的面积=

DE

和弦DE围成的部分的面积是解答本题的关键．