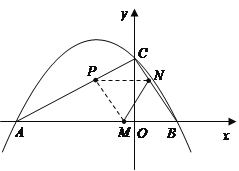
题目内容
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 向点
向点![]() 匀速运动,速度是
匀速运动,速度是![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,同时,点
,同时,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向,在射线
方向,在射线![]() 上匀速运动,速度是
上匀速运动,速度是![]() ,连接
,连接![]() 、
、![]() ,
,![]() 与
与![]() 交与点
交与点![]() ,设运动时间为
,设运动时间为![]() .
.
(1)当![]() 为何值时,四边形
为何值时,四边形![]() 是平行四边形;
是平行四边形;
(2)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)是否存在某一时刻![]() ,使得
,使得![]() 的面积为矩形
的面积为矩形![]() 面积的
面积的![]() ;
;
(4)是否存在某一时刻![]() ,使得点
,使得点![]() 在线段
在线段![]() 的垂直平分线上.
的垂直平分线上.
【答案】(1)![]() ;(2)
;(2)![]()
![]() ;(3)当
;(3)当![]() 或
或![]() 时,
时,![]() 的面积为矩形
的面积为矩形![]() 面积的
面积的![]() ;(4)当
;(4)当![]() 时,点
时,点![]() 在线段
在线段![]() 的垂直平分线上
的垂直平分线上
【解析】
(1)由四边形![]() 是平行四边形,可得
是平行四边形,可得![]() 由
由![]() 得四边形
得四边形![]() 为平行四边形,即
为平行四边形,即![]() ,列式
,列式![]() ,计算可解.
,计算可解.
(2)由![]() ,得
,得![]() ,代入时间
,代入时间![]() ,得
,得![]() 解得
解得![]() ,
,![]()
再通过![]() 梯形
梯形![]() 构建联系,可列函数式
构建联系,可列函数式![]() .
.
(3)由![]() 的面积为矩形
的面积为矩形![]() 面积的
面积的![]() 得
得![]() ,可解
,可解
当![]() 或
或![]() 时,
时,![]() 的面积为矩形
的面积为矩形![]() 面积的
面积的![]() .
.
(4)当点![]() 在线段
在线段![]() 的垂直平分线上时,
的垂直平分线上时,![]() ,得
,得![]() ,由
,由![]() 与
与 ![]() 可得,
可得,![]() ,
,![]() ,即
,即![]() ,代入
,代入![]() ,
,![]() ,
,![]() ,
,![]()
可得![]() ,计算验证可解.
,计算验证可解.
(1)当四边形![]() 是平行四边形时,
是平行四边形时,![]() ,
,
又∵![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
即![]() ,
,
∴![]()
(2)∵![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
![]() 梯形
梯形![]() ,
,
∴![]() 梯形
梯形![]()
(3)由题意,![]()
解得![]() ,
,![]()
所以当![]() 或
或![]() 时,
时,![]() 的面积为矩形
的面积为矩形![]() 面积的
面积的![]() .
.
(4)当点![]() 在线段
在线段![]() 的垂直平分线上时,
的垂直平分线上时,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
即![]()
解得![]() ,
,![]() (舍)
(舍)
所以当![]() 时,点
时,点![]() 在线段
在线段![]() 的垂直平分线上.
的垂直平分线上.

【题目】某校门口竖着“前方学校,减速慢行”的交通指示牌CD,数学“综合与实践”小组的同学将“测量交通指示牌CD的高度”作为一项课题活动,他们定好了如下测量方案:
项目 | 内容 |
课题 | 测量交通指示牌CD的高度 |
测量示意图 |
|
测量步骤 | (1)从交通指示牌下的点M处出发向前走10 米到达A处; (2)在点A处用量角仪测得∠DAM=27°; (3)从点A沿直线MA向前走10米到达B处;(4)在点B处用量角仪测得∠CBA=18°. |
请你帮助该小组同学根据上表中的测量数据,求出交通指示牌CD的高度.(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)