Question

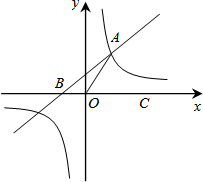（2013•东营）如图，在平面直角坐标系中，一次函数y=nx+2（n≠0）的图象与反比例函数y=

m

x

(m≠0)在第一象限内的图象交于点A，与x轴交于点B，线段OA=5，C为x轴正半轴上一点，且sin∠AOC=

4

5

．
（1）求一次函数和反比例函数的解析式；
（2）求△AOB的面积．

Answer 1

分析：（1）过A点作AD⊥x轴于点D，根据已知的∠AOC的正弦值以及OA的长，利用三角形函数的定义求出AD的长，再利用勾股定理求出OD的长，即可得到点A的坐标，把点A的坐标分别代入到反比例函数和一次函数的解析式中即可确定出两函数的解析式；
（2）根据x轴上点的特征，令一次函数的y=0，求出x的值，确定出点B的坐标，得到线段OB的长，利用三角形的面积公式即可求出三角形AOB的面积．

解答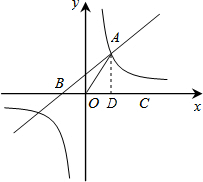：解：（1）过A点作AD⊥x轴于点D，
∵sin∠AOC=

AD

AO

=

4

5

，OA=5，
∴AD=4，
在Rt△AOD中，由勾股定理得：DO=3，
∵点A在第一象限，
∴点A的坐标为（3，4），
将A的坐标为（3，4）代入y=

m

x

，得4=

m

3

，
∴m=12，
∴该反比例函数的解析式为y=

12

x

，
将A的坐标为（3，4）代入y=nx+2得：n=

2

3

，
∴一次函数的解析式是y=

2

3

x+2；

（2）在y=

2

3

x+2中，令y=0，即

2

3

x+2=0，
∴x=-3，
∴点B的坐标是（-3，0）
∴OB=3，又AD=4，
∴S_△AOB=

1

2

OB•AD=

1

2

×3×4=6，
则△AOB的面积为6．

点评：此题考查了反比例函数与一次函数的交点问题，涉及的知识有：勾股定理，待定系数法求函数的解析式，三角形的面积，以及三角函数的定义，用待定系数法确定函数的解析式，是常用的一种解题方法，同学们要熟练掌握这种方法．