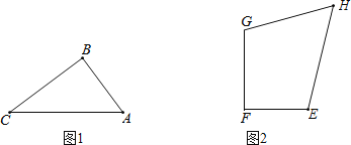Question

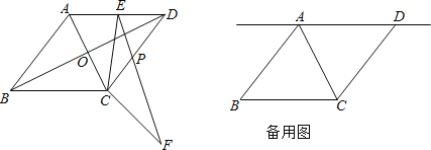
【题目】如图，在菱形ABCD中，对角线AC、BD交于点O，已知AC=2，AB=5．

（1）求BD的长；

（2）点E为直线AD上的一个动点，连接CE，将线段EC绕点C顺时针旋转∠BCD的角度后得到对应的线段CF（即∠ECF=∠BCD），EF交CD于点P．

①当E为AD的中点时，求EF的长；

②连接AF、DF，当DF的长度最小时，求△ACF的面积．

Answer 1

【答案】（1）BD=4；（2）①EF=2；②当DF的长度最小时，△ACF的面积为14．

【解析】

（1）由菱形的性质得出AD=AB=BC=CD=5，AC⊥BD，由勾股定理求出OB，即可得出BD的长；

（2）①过点C作CH⊥AD于H，由菱形的性质和三角函数得出求出AH=2，由勾股定理求出求出再由勾股定理求出证明△BCD∽△ECF，得出即可得出结果；

②先证明△BCE≌△DCF，得出BE=DF，当BE最小时，DF就最小，且BE⊥DE时，BE最小，此时∠EBC=∠FDC=90°，BE=DF=4，△EBC的面积=△ABC的面积=△DCF的面积，则四边形ACFD的面积=2△ABC的面积=20，过点F作FH⊥AD于H，过点C作CP⊥AD于P，则∠CPD=90°，证明△PCD∽△HDF，得出求出即可得出△ACF的面积．

（1）∵四边形ABCD是菱形，

∴AD=AB=BC=CD=5，AC⊥BD，OA=OC=AC=，OB=OD，

在Rt△ABO中，由勾股定理得：OB===2，

∴BD=2OB=4；

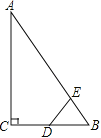
（2）①过点C作CH⊥AD于H，如图1所示：

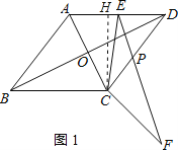
∵四边形ABCD是菱形，

∴∠BAC=∠DAC，

∴cos∠BAC=cos∠DAC，

∴==，即=，

∴AH=2，

∴CH==4，

∵E为AD的中点，

∴AE=AD=，

∴HE=AE-AH=，

在Rt△CHE中，由勾股定理得：EC==，

由旋转的性质得：∠ECF=∠BCD，CF=CE，

∴=，

∴△BCD∽△ECF，

∴，即=，

解得：EF=2；

②如图2所示：

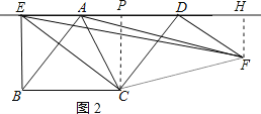
∵∠BCD=∠ECF，

∴∠BCD-DCE=∠ECF-∠DCE，即∠BCE=∠DCF，

在△BCE和△DCF中，，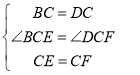

∴△BCE≌△DCF（SAS），

∴BE=DF，

当BE最小时，DF就最小，且BE⊥DE时，BE最小，

此时∠EBC=∠FDC=90°，BE=DF=4，△EBC的面积=△ABC的面积=△DCF的面积，

则四边形ACFD的面积=2△ABC的面积=5×4=20，

过点F作FH⊥AD于H，过点C作CP⊥AD于P，

则∠CPD=90°，

∴∠PCD+∠PDC=90°，

∵∠FDC=90°，

∴∠PDC+∠HDF=90°，

∴∠PCD=∠HDF，

∴△PCD∽△HDF，

∴==，

∴HF=4×=，

∴△ADF的面积=ADHF=×5×=6，

∴△ACF的面积=四边形ACFD的面积-△ADF的面积=20-6=14，

即当DF的长度最小时，△ACF的面积为14．