题目内容
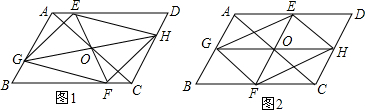
2.如图1,?ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E,F,GH过点O,与AB,CD分别相交于点G,H,连接EG,FG,FH,EH.(1)求证:四边形EGFH是平行四边形;
(2)如图2,若EF∥AB,GH∥BC,在不添加任何辅助线的情况下,请直接写出图2中与四边形AGHD面积相等的所有平行四边形(四边形AGHD除外).
分析 (1)由四边形ABCD是平行四边形,得到AD∥BC,根据平行四边形的性质得到∠EAO=∠FCO,证出△OAE≌△OCF,得到OE=OF,同理OG=OH,根据对角线互相平分的四边形是平行四边形得到结论;
(2)根据两组对边分别平行的四边形是平行四边形即可得到结论.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAO=∠FCO,
在△OAE与△OCF中$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{∠AOE=∠COF}\\{OA=OC}\end{array}\right.$,
∴△OAE≌△OCF,
∴OE=OF,
同理OG=OH,
∴四边形EGFH是平行四边形;
(2)解:与四边形AGHD面积相等的所有平行四边形有?GBCH,?ABFE,?EFCD,?EGFH;
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∵EF∥AB,GH∥BC,
∴四边形GBCH,ABFE,EFCD,EGFH为平行四边形,
∵EF过点O,GH过点O,
∵OE=OF,OG=OH,
∴?GBCH,?ABFE,?EFCD,?EGFH,?ACHD它们面积=$\frac{1}{2}$?ABCD的面积,
∴与四边形AGHD面积相等的所有平行四边形有?GBCH,?ABFE,?EFCD,?EGFH.
点评 本题考查了平行四边形的判定和性质,全等三角形的判定和性质,熟练掌握平行四边形的判定定理是解题的关键.

练习册系列答案
相关题目
12.计算(-π)0,结果是( )
| A. | 0 | B. | -π | C. | -3.14 | D. | 1 |
10. 在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①S甲2>S乙2;②S甲2<S乙2;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定,由统计图可知正确的结论是( )
在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①S甲2>S乙2;②S甲2<S乙2;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定,由统计图可知正确的结论是( )
 在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①S甲2>S乙2;②S甲2<S乙2;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定,由统计图可知正确的结论是( )
在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①S甲2>S乙2;②S甲2<S乙2;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定,由统计图可知正确的结论是( )| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
12. 如图所示的几何体,其左视图是( )
如图所示的几何体,其左视图是( )
 如图所示的几何体,其左视图是( )
如图所示的几何体,其左视图是( )| A. |  | B. |  | C. |  | D. |  |
 如图,把△EFP按图示方式放置在菱形ABCD中,使得顶点E、F、P分别在线段AB、AD、AC上,已知EP=FP=4,EF=4$\sqrt{3}$,∠BAD=60°,且AB>4$\sqrt{3}$.
如图,把△EFP按图示方式放置在菱形ABCD中,使得顶点E、F、P分别在线段AB、AD、AC上,已知EP=FP=4,EF=4$\sqrt{3}$,∠BAD=60°,且AB>4$\sqrt{3}$.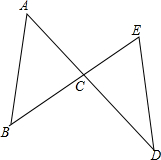 如图所示,∠A=50°,∠B=45°,∠D=35°,求∠E的度数.
如图所示,∠A=50°,∠B=45°,∠D=35°,求∠E的度数. 如图所示的容器内装满水,打开排水管,容器内的水匀速流出,则容器内液面的高度h随时间x变化的函数图象最接近实际情况的是( )
如图所示的容器内装满水,打开排水管,容器内的水匀速流出,则容器内液面的高度h随时间x变化的函数图象最接近实际情况的是( )


