Question

（2011•葫芦岛）如图，在4×5网格图中，其中每个小正方形边长均为1，梯形ABCD和五边形EFGHK的顶点均为小正方形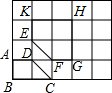的顶点．
（1）以B为位似中心，在网格图中作四边形A′BC′D′，使四边形A′BC′D′和梯形ABCD位似，且位似比为2：1；
（2）求（1）中四边形A′BC′D′与五边形EFGHK重叠部分的周长．（结果保留根号）

Answer 1

分析：（1）分别延长BA、BC、BD到A′、C′、D′，使BA′=2BA，BC′=2BC，BD′=2BD，然后顺次连接A′BC′D′即可得解；
（2）根据网格图形，重叠部分正好是以格点为顶点的平行四边形，求出两邻边的长的，然后根据平行四边形的周长公式计算即可．

解答：解：（1）如图所示：四边形A′BC′D′就是所要求作的梯形；


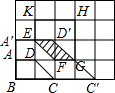
（2）四边形A′BC′D′与五边形EFGHK重叠部分是平行四边形EFGD′，ED′=FG=1，
在Rt△EDF中，ED=DF=1，
由勾股定理得EF=

12+12

=

2

，
∴D′G=EF=

2

，
∴四边形A′BC′D′与五边形EFGHK重叠部分的周长=ED′+FG+D′G+EF，
=1+1+

2

+

2

，
=2+2

2

．
故答案为：2+2

2

．

点评：本题考查了利用位似变换作图，关键是根据位似变换的定义找出点A、C、D的对应点的位置．