ƒøƒ⁄»ð
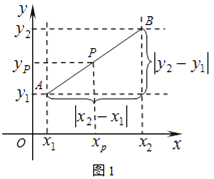
°æƒø°ø‘ƒ∂¡≤ƒ¡œ£∫»ÁÕº1£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨A°¢B¡Ωµ„µƒ◊¯±Í∑÷±Œ™A£®x1 £¨ y1£©£¨B£®x2£¨y2£©£¨AB÷–µ„Pµƒ◊¯±ÍŒ™£®xp£¨yp£©£Æ”…xp©Åx1=x2©Åxp£¨µ√xp= ![]() £¨Õ¨¿Ìyp=
£¨Õ¨¿Ìyp= ![]() £¨À˘“‘ABµƒ÷–µ„◊¯±ÍŒ™£®
£¨À˘“‘ABµƒ÷–µ„◊¯±ÍŒ™£®![]() £¨
£¨![]() £©£Æ”…π¥π…∂®¿Ìµ√AB2=|x2©Åx1|2+|y2©Åy1|2£¨À˘“‘A°¢B¡Ωµ„º‰µƒæý¿Îπ´ ΩŒ™AB=
£©£Æ”…π¥π…∂®¿Ìµ√AB2=|x2©Åx1|2+|y2©Åy1|2£¨À˘“‘A°¢B¡Ωµ„º‰µƒæý¿Îπ´ ΩŒ™AB=![]() £Æ’‚¡Ωπ´ Ω∂‘A°¢B‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–∆‰À¸Œª÷√“≤≥…¡¢£ÆΩ‚¥œ¬¡–Œ £∫
£Æ’‚¡Ωπ´ Ω∂‘A°¢B‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–∆‰À¸Œª÷√“≤≥…¡¢£ÆΩ‚¥œ¬¡–Œ £∫
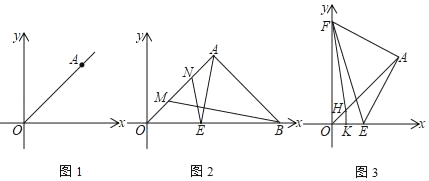
£®1£©“—÷™M£®1£¨©Å2£©£¨N£®©Å1£¨2£©£¨÷±Ω”¿˚”√π´ ΩÃÓø’£∫MN÷–µ„◊¯±ÍŒ™________£¨MN=________£Æ
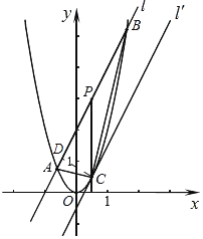
£®2£©»ÁÕº2£¨÷±œþl£∫y=2x+2”Î≈◊ŒÔœþy=2x2Ωª”⁄A°¢B¡Ωµ„£¨PŒ™ABµƒ÷–µ„£¨π˝P◊˜x÷·µƒ¥πœþΩª≈◊ŒÔœþ”⁄µ„C£Æ
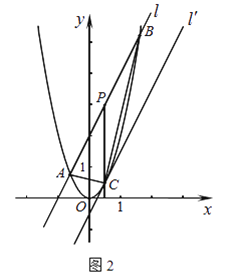
£®a£©«ÛA°¢B¡Ωµ„µƒ◊¯±Íº∞Cµ„µƒ◊¯±Í£ª
£®b£©¡¨Ω·AB°¢AC£¨«Û÷§°˜ABCŒ™÷±Ω«»˝Ω«–Œ£ª
£®c£©Ω´÷±œþl∆Ω“∆µΩCµ„ ±µ√µΩ÷±œþl°‰£¨«Û¡Ω÷±œþl”Îl°‰µƒæý¿Î.
°æ¥∞∏°ø£®1£©£®0£¨0£©£ª2![]() £ª£®2£©£®a£©A£®
£ª£®2£©£®a£©A£® ![]() £¨3©Å
£¨3©Å![]() £©£ªB£®
£©£ªB£® ![]() £¨3+
£¨3+![]() £©£ª C£®
£©£ª C£® ![]() £¨
£¨![]() £©£ª£®b£©÷§√˜º˚Ω‚Œˆ£ª£®c£©
£©£ª£®b£©÷§√˜º˚Ω‚Œˆ£ª£®c£©![]() .
.
°æΩ‚Œˆ°ø
£®1£©∏˘æð÷–µ„◊¯±Íπ´ Ω£¨¡Ωµ„º‰µƒæý¿Îπ´ Ω£¨ø…µ√¥∞∏£ª
£®a£©∏˘æðΩ‚∑Ω≥Ã◊È£¨ø…µ√A£¨Bµ„◊¯±Í£¨∏˘æð÷–µ„◊¯±Íπ´ Ω£¨ø…µ√Pµ„◊¯±Í£¨∏˘æð∆Ω––”⁄y÷·µƒ÷±œþ∫·◊¯±Íœýµ»£¨ø…µ√Cµ„∫·◊¯±Í£¨∏˘æð◊‘±‰¡ø”Î∫Ø ˝÷µµƒ∂‘”¶πÿœµ£¨ø…µ√Cµ„◊¯±Í£ª
£®b£©∏˘æðπ¥π…∂®¿Ìº∞π¥π…∂®¿ÌµƒƒÊ∂®¿Ì£¨ø…µ√¥∞∏£ª
£®c£©∏˘æð»˝Ω«–Œµƒ√ʪ˝≤ªÕ¨±Ì 棨ø…µ√πÿ”⁄CDµƒ∑Ω≥ã¨∏˘æðΩ‚∑Ω≥ã¨ø…µ√¥∞∏£Æ
£®1£©£®0£¨0£©£ª2![]()
£®2£©Ω‚£∫£®a£©¡™¡¢÷±œþ°¢≈◊ŒÔœþ£¨µ√ ![]() £¨
£¨
Ω‚µ√ 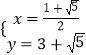 £¨
£¨ 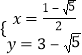 £¨
£¨
º¥B£® ![]() £¨3+
£¨3+![]() £©£¨A£®
£©£¨A£® ![]() £¨3©Å
£¨3©Å![]() £©£Æ
£©£Æ
”…P «ABµƒ÷–µ„£¨µ√
P£® ![]() £¨3£©
£¨3£©
µ±x= ![]() ±£¨y=2x2=
±£¨y=2x2= ![]() £¨º¥Cµ„◊¯±ÍŒ™£®
£¨º¥Cµ„◊¯±ÍŒ™£® ![]() £¨
£¨ ![]() £©£Æ
£©£Æ
£®b£©AB2=£® ![]() ©Å
©Å ![]() £©2+£®3+
£©2+£®3+ ![]() ©Å3+
©Å3+ ![]() £©2=25£ª
£©2=25£ª
BC2=£® ![]() ©Å
©Å ![]() £©2+£®3+
£©2+£®3+ ![]() ©Å
©Å ![]() £©2=
£©2= ![]() ©Å5
©Å5 ![]() £ª
£ª
AC2=£® ![]() ©Å
©Å ![]() £©2+£®3©Å
£©2+£®3©Å ![]() ©Å
©Å ![]() £©2=
£©2= ![]() +5
+5 ![]() £¨
£¨
°þAC2+BC2=AB2 £¨
°ý°œACB=90°„
°ý°˜ABC «÷±Ω«»˝Ω«–Œ£ª
£®c£©»ÁÕº
◊˜CD°ÕAB”⁄Dµ„£¨CD «¡Ω÷±œþº‰µƒæý¿Î£¨
S°˜ABC= ![]() ABCD=
ABCD= ![]() ACBC£¨
ACBC£¨
![]() °¡5CD=
°¡5CD= ![]() °¡
°¡ ![]() £¨
£¨
Ω‚µ√CD= ![]() £Æ
£Æ
¡Ω÷±œþl”Îl°‰µƒæý¿Î « ![]()