题目内容
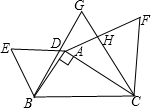如图，以Rt△ABC的三边向外作正△ABE、正△GBC、正△ACF，且AB=3，AC=4，则S△BED+S△CHF-S四边形ADGH=分析：把所求的面积的和差分别表示为：
S△ABE-S△ABD+S△AFC-S△AHC-S四边形ADGH
=S△ABE+S△AFC-（S△ABD+S△AHC+S四边形ADGH）
=S△ABE+S△AFC+S△ABC-S△BCG，分别代入面积求解即可．
S△ABE-S△ABD+S△AFC-S△AHC-S四边形ADGH
=S△ABE+S△AFC-（S△ABD+S△AHC+S四边形ADGH）
=S△ABE+S△AFC+S△ABC-S△BCG，分别代入面积求解即可．
解答：解：∵∠BAC=90°，AB=3，AC=4，
∴BC=5，
∴S△ABE=
，S△AFC=4
，S△ABC=6，S△BCG=
，
∵S△BED+S△CHF-S四边形ADGH
=S△ABE-S△ABD+S△AFC-S△AHC-S四边形ADGH
=S△ABE+S△AFC-（S△ABD+S△AHC+S四边形ADGH）
=S△ABE+S△AFC+S△ABC-S△BCG
=
+4
+6-
=6．
∴应填6．
∴BC=5，
∴S△ABE=
9
| ||
| 4 |
| 3 |
25
| ||
| 4 |
∵S△BED+S△CHF-S四边形ADGH
=S△ABE-S△ABD+S△AFC-S△AHC-S四边形ADGH
=S△ABE+S△AFC-（S△ABD+S△AHC+S四边形ADGH）
=S△ABE+S△AFC+S△ABC-S△BCG
=
9
| ||
| 4 |
| 3 |
25
| ||
| 4 |
=6．
∴应填6．
点评：本题需要将所求的问题进行转化，根据图形的特点，将复杂的问题转化成简单的问题来解决．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
23、如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连接ED、BD．
如图，以Rt△ABC各边为直径的三个半圆围成两个新月形（阴影部分），已知AC=3cm，BC=4cm．则新月形（阴影部分）的面积和是
已知，如图，以Rt△ABC的斜边AB为直径作⊙0，D是BC上的点，且有弧AC=弧CD，连CD、BD，在BD延长线上取一点E，使∠DCE=∠CBD．
如图，以Rt△ABC的直角边AC为直径作圆O交斜边AB于点D，若劣弧CD=120°，则
（2009•黔南州）如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连接DE．