题目内容
已知⊙O是以原点为圆心, 为半径的圆,点P是直线
为半径的圆,点P是直线 上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为(
)
上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为(
)

A.3
B.4 C. D.
D.
【答案】
B.
【解析】
试题分析:由P在直线 上,设
上,设 ,连接OQ,OP,由PQ为圆O的切线,得到PQ⊥OQ,在Rt△OPQ中,利勾股定理列出关系式,配方后利用二次函数的性质即可求出PQ的最小值:
,连接OQ,OP,由PQ为圆O的切线,得到PQ⊥OQ,在Rt△OPQ中,利勾股定理列出关系式,配方后利用二次函数的性质即可求出PQ的最小值:
∵P在直线 上,∴设P坐标为
上,∴设P坐标为 ,
,
连接OQ,OP,由PQ为圆O的切线,得到PQ⊥OQ,
在Rt△OPQ中,根据勾股定理得:OP2=PQ2+OQ2,
∵OQ= ,∴
,∴ .
.
则当m=3时, 取得最小值16,∴切线长PQ的最小值为4.
取得最小值16,∴切线长PQ的最小值为4.
故选B.

考点:1.一次函数综合题,2.直线上点的坐标与方程的关系;3. 勾股定理;4. 二次函数的最值.

练习册系列答案
相关题目
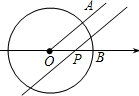 如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是( )
如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是( )A、O<x≤
| ||||
B、-
| ||||
| C、-1≤x≤1 | ||||
D、x>
|
 如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P(P与O不重合)在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设点P所表示的实数为x,则x的取值范围是( )
如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P(P与O不重合)在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设点P所表示的实数为x,则x的取值范围是( )| A、-1≤x<0或0<x≤1 | ||||
B、0<x≤
| ||||
C、-
| ||||
D、x>
|
 如图,已知⊙O是以数轴的原点为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行(或重合)的直线l与⊙O有公共点,设点P在数轴上对应的数值为a,则a的取值范围是
如图,已知⊙O是以数轴的原点为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行(或重合)的直线l与⊙O有公共点,设点P在数轴上对应的数值为a,则a的取值范围是 如图,已知⊙O是以坐标原点O为圆心,1为半径的圆,在此直角坐标系中画直线y=kx+2,若直线y=kx+2与⊙O相切,则k=
如图,已知⊙O是以坐标原点O为圆心,1为半径的圆,在此直角坐标系中画直线y=kx+2,若直线y=kx+2与⊙O相切,则k=