题目内容
 如图,已知⊙O是以数轴的原点为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行(或重合)的直线l与⊙O有公共点,设点P在数轴上对应的数值为a,则a的取值范围是
如图,已知⊙O是以数轴的原点为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行(或重合)的直线l与⊙O有公共点,设点P在数轴上对应的数值为a,则a的取值范围是-
≤a≤
且a不等于0
| 2 |
| 2 |
-
≤a≤
且a不等于0
.| 2 |
| 2 |
分析:根据过点P且与OA平行的直线与⊙O相切时,假设切点为D,得出OD=DP=1,进而得出OP的取值范围.
解答:解:∵⊙O是以数轴的原点为圆心,半径为1的圆,∠AOB=45°,
∴过点P′且与OA平行的直线与⊙O相切时,假设切点为D,
∴OD=DP′=1,
OP′=
,
∴0<OP≤
,
同理可得,当OP与x轴负半轴相交时,
-
≤OP<0,
∴-
≤OP<0,或0<OP≤
.
故答案为:-
≤a≤
且a不等于0.
∴过点P′且与OA平行的直线与⊙O相切时,假设切点为D,

∴OD=DP′=1,
OP′=
| 2 |
∴0<OP≤
| 2 |
同理可得,当OP与x轴负半轴相交时,
-
| 2 |
∴-
| 2 |
| 2 |
故答案为:-
| 2 |
| 2 |
点评:此题主要考查了直线与圆的位置关系,分别得出两圆与圆相切时求出P点的坐标是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 24、如图,直线CD经过线段AB的一个端点B,∠ABC=50°,点P为直线CD上一点;已知△PAB是以AB为底边的等腰三角形,⊙O是以AB为直径的圆.
24、如图,直线CD经过线段AB的一个端点B,∠ABC=50°,点P为直线CD上一点;已知△PAB是以AB为底边的等腰三角形,⊙O是以AB为直径的圆. 如图,已知⊙O是以数轴原点O为原点,半径为2的圆,∠AOB=60°,点P是在数轴上运动的动点,若过P且与OA平行(或重合)的直线l与⊙O有公共点,求动点P所表示的数的取值范围.
如图,已知⊙O是以数轴原点O为原点,半径为2的圆,∠AOB=60°,点P是在数轴上运动的动点,若过P且与OA平行(或重合)的直线l与⊙O有公共点,求动点P所表示的数的取值范围. 如图,已知A、B、C是数轴上三点,点C表示的数为6,BC=4,AB=12.
如图,已知A、B、C是数轴上三点,点C表示的数为6,BC=4,AB=12. 如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)
如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)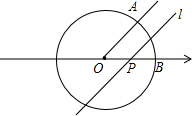 如图,已知⊙O是以数轴原点O为原点,半径为2的圆,∠AOB=60°,点P是在数轴上运动的动点,若过P且与OA平行(或重合)的直线l与⊙O有公共点,求动点P所表示的数的取值范围.
如图,已知⊙O是以数轴原点O为原点,半径为2的圆,∠AOB=60°,点P是在数轴上运动的动点,若过P且与OA平行(或重合)的直线l与⊙O有公共点,求动点P所表示的数的取值范围.