ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥ΙΪΥΨΙΚΫχΡ≥÷÷Υ°ΙϊΒΡ≥…±ΨΈΣ![]() ‘Σ/«ßΩΥΘ§Ψ≠Ιΐ –≥ΓΒς―–ΖΔœ÷Θ§’β÷÷Υ°Ιϊ‘ΎΈ¥ά¥
‘Σ/«ßΩΥΘ§Ψ≠Ιΐ –≥ΓΒς―–ΖΔœ÷Θ§’β÷÷Υ°Ιϊ‘ΎΈ¥ά¥![]() ΧλΒΡœζ έΦέΗώ
ΧλΒΡœζ έΦέΗώ![]() Θ®‘Σ/«ßΩΥΘ©”κ ±Φδ
Θ®‘Σ/«ßΩΥΘ©”κ ±Φδ![]() Θ®ΧλΘ©÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΈΣ
Θ®ΧλΘ©÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΈΣ
 Θ§«“Τδ»’œζ έΝΩ
Θ§«“Τδ»’œζ έΝΩ![]() Θ®«ßΩΥΘ©”κ ±Φδ
Θ®«ßΩΥΘ©”κ ±Φδ![]() Θ®ΧλΘ©ΒΡΙΊœΒ»γœ¬±μΘΚ
Θ®ΧλΘ©ΒΡΙΊœΒ»γœ¬±μΘΚ
±Φδ |
|
|
|
|
|
| Γ≠ |
»’œζ έΝΩ |
|
|
|
|
|
| Γ≠ |
![]() “―÷Σ
“―÷Σ![]() ”κ
”κ![]() ÷°ΦδΒΡ±δΜ·Ιφ¬…ΖϊΚœ“Μ¥ΈΚ· ΐΙΊœΒΘ§ ‘«σ‘ΎΒΎ
÷°ΦδΒΡ±δΜ·Ιφ¬…ΖϊΚœ“Μ¥ΈΚ· ΐΙΊœΒΘ§ ‘«σ‘ΎΒΎ![]() ΧλΒΡ»’œζ έΝΩ «Εύ…ΌΘΩ
ΧλΒΡ»’œζ έΝΩ «Εύ…ΌΘΩ
![]() Έ ΡΡ“ΜΧλΒΡœζ έάϊ»σΉν¥σΘΩΉν¥σ»’œζ έάϊ»σΈΣΕύ…ΌΘΩ
Έ ΡΡ“ΜΧλΒΡœζ έάϊ»σΉν¥σΘΩΉν¥σ»’œζ έάϊ»σΈΣΕύ…ΌΘΩ
![]() ‘Ύ ΒΦ œζ έΒΡ«Α
‘Ύ ΒΦ œζ έΒΡ«Α![]() Χλ÷–Θ§ΙΪΥΨΨωΕ®ΟΩœζ έ
Χλ÷–Θ§ΙΪΥΨΨωΕ®ΟΩœζ έ![]() «ßΩΥΥ°ΙϊΨΆΨη‘υ
«ßΩΥΥ°ΙϊΨΆΨη‘υ![]() ‘Σάϊ»σ
‘Σάϊ»σ![]() ΗχΓΑΨΪΉΦΖωΤΕΓ±Ε‘œσΘ°œ÷ΖΔœ÷ΘΚ‘Ύ«Α
ΗχΓΑΨΪΉΦΖωΤΕΓ±Ε‘œσΘ°œ÷ΖΔœ÷ΘΚ‘Ύ«Α![]() Χλ÷–Θ§ΟΩΧλΩέ≥ΐΨη‘υΚσΒΡ»’œζ έάϊ»σΥφ ±Φδ
Χλ÷–Θ§ΟΩΧλΩέ≥ΐΨη‘υΚσΒΡ»’œζ έάϊ»σΥφ ±Φδ![]() ΒΡ‘ω¥σΕχ‘ω¥σΘ§«σ
ΒΡ‘ω¥σΕχ‘ω¥σΘ§«σ![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
ΓΨ¥πΑΗΓΩ(1) ‘ΎΒΎ![]() ΧλΒΡ»’œζ έΝΩ «
ΧλΒΡ»’œζ έΝΩ «![]() Θ°(2) ΒΎ
Θ°(2) ΒΎ![]() Χλάϊ»σΉν¥σΘ§Ήν¥σάϊ»σΈΣ
Χλάϊ»σΉν¥σΘ§Ήν¥σάϊ»σΈΣ![]() ‘ΣΘ°(3)
‘ΣΘ°(3)![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
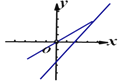
(1)ΗυΨί»’œζ έΝΩy”κ ±ΦδtΒΡΙΊœΒ±μΘ§…ηyΘΫktΘΪbΘ§ΫΪ±μ÷– ΐ÷Β¥ζ»κΦ¥Ω…«σ≥ω“Μ¥ΈΚ· ΐΫβΈω ΫΘ§‘ΌΫΪt ΘΫ30¥ζ»κ“Μ¥ΈΚ· ΐΒΡΫβΈω Ϋ÷–Θ§Φ¥Ω…«σ≥ωΒΎ30ΧλΒΡ»’œζΝΩΘΜ(2)άϊ»σΘΫ( έΦέΘ≠≥…±Ψ)ΓΝœζ έΝΩΘ§Ζ÷1ΓήtΓή24ΚΆ25ΓήtΓή48ΝΫ÷÷«ιΩωΘ§Α¥’’ΧβΡΩΗχ≥ωΒΡ έΦέΚΆ ±Φδ÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΖ÷±πΒΟ≥ωœζ έάϊ»σΒΡΙΊœΒ ΫΘ§‘ΌΆ®ΙΐΕΰ¥ΈΚ· ΐΆΦœσΒΡ–‘÷ Φ¥Ω…«σ≥ωΉν¥σ÷ΒΘ§±»ΫœΒΟ≥ωΫαΙϊΘΜ(3)ΗυΨίΧβ“βΝ–≥ωΙΊ”Ύάϊ»σΒΡΕΰ¥ΈΚ· ΐΘ§ΒΟΒΫΕΰ¥ΈΚ· ΐΈΣΩΣΩΎœρœ¬Θ§Ε‘≥Τ÷αΈΣtΘΫ2nΘΪ10ΒΡ≈ΉΈοœΏΘ§“Σ Ιάϊ»σΥφtΒΡ‘ω¥σΕχ‘ω¥σΘ§‘ρ2nΘΪ10Γί24Θ§Φ¥Ω…ΒΟ≥ωnΒΡ»Γ÷ΒΖΕΈß.
![]() …η
…η![]() Θ§Α―
Θ§Α―![]() Θ§
Θ§![]() ΘΜ
ΘΜ![]() Θ§
Θ§![]() ¥ζ»κΒΟΒΫΘΚ
¥ζ»κΒΟΒΫΘΚ
![]() Θ§
Θ§
ΫβΒΟΘΚ![]() Θ§
Θ§
Γύ![]() Θ°
Θ°
ΫΪ![]() ¥ζ»κ…œ ΫΘ§ΒΟΘΚ
¥ζ»κ…œ ΫΘ§ΒΟΘΚ![]() Θ°
Θ°
Υυ“‘‘ΎΒΎ![]() ΧλΒΡ»’œζ έΝΩ «
ΧλΒΡ»’œζ έΝΩ «![]() Θ°
Θ°
![]() …ηΒΎ
…ηΒΎ![]() ΧλΒΡœζ έάϊ»σΈΣ
ΧλΒΡœζ έάϊ»σΈΣ![]() ‘ΣΘ°
‘ΣΘ°
Β±![]() ±Θ§”…Χβ“β
±Θ§”…Χβ“β![]() Θ§
Θ§
Γύ![]() ±
±![]() Ήν¥σ÷ΒΈΣ
Ήν¥σ÷ΒΈΣ![]() ‘ΣΘ°
‘ΣΘ°
Β±![]() ±Θ§
±Θ§![]() Θ§
Θ§
ΓΏΕ‘≥Τ÷α![]() Θ§
Θ§![]() Θ§
Θ§
Γύ‘ΎΕ‘≥Τ÷αΉσ≤ύ![]() Υφ
Υφ![]() ‘ω¥σΕχΦθ–ΓΘ§
‘ω¥σΕχΦθ–ΓΘ§
Γύ![]() ±Θ§
±Θ§![]() Ήν¥σ÷Β
Ήν¥σ÷Β![]() Θ§
Θ§
Ήέ…œΥυ ωΒΎ![]() Χλάϊ»σΉν¥σΘ§Ήν¥σάϊ»σΈΣ
Χλάϊ»σΉν¥σΘ§Ήν¥σάϊ»σΈΣ![]() ‘ΣΘ°
‘ΣΘ°
![]() …ηΟΩΧλΩέ≥ΐΨη‘υΚσΒΡ»’œζ έάϊ»σΈΣ
…ηΟΩΧλΩέ≥ΐΨη‘υΚσΒΡ»’œζ έάϊ»σΈΣ![]() ‘ΣΘ°
‘ΣΘ°
”…Χβ“β Θ§
Θ§
ΓΏ‘Ύ«Α![]() Χλ÷–Θ§ΟΩΧλΩέ≥ΐΨη‘υΚσΒΡ»’œζ έάϊ»σΥφ ±Φδ
Χλ÷–Θ§ΟΩΧλΩέ≥ΐΨη‘υΚσΒΡ»’œζ έάϊ»σΥφ ±Φδ![]() ΒΡ‘ω¥σΕχ‘ω¥σΘ§
ΒΡ‘ω¥σΕχ‘ω¥σΘ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ°
Θ°
”÷ΓΏ![]() Θ§
Θ§
Γύ![]() ΒΡ»Γ÷ΒΖΕΈßΈΣ
ΒΡ»Γ÷ΒΖΕΈßΈΣ![]() Θ°
Θ°

 ΒΎ1ΨμΒΞ‘Σ‘¬ΩΦΤΎ÷–ΤΎΡ©œΒΝ–¥πΑΗ
ΒΎ1ΨμΒΞ‘Σ‘¬ΩΦΤΎ÷–ΤΎΡ©œΒΝ–¥πΑΗ