题目内容
如图，在6×6的正方形网格中，每个小正方形的边长都是1，△ABC的三个顶点都在格点（即小正方形的顶点）上．
（1）画出线段AC平移后的线段BD，其平移方向为射线AB的方向，平移的距离为线段AB的长；
（2）求sin∠DBC的值．
解：（1）如图．
（2）在△ABC中，
AB=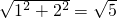
，BC=
，AC=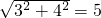
．
则AB2+BC2=AC2，
∴△ABC是直角三角形，∠ABC=90°
∴sin∠BCA=
∵线段BD是由线段AC平移得到的，
∴BD∥AC，
∴∠DBC=∠BCA，
∴sin∠DBC=sin∠BCA=
．
分析：（1）直接平移A，C两点，再根据平移方向为射线AB的方向，平移的距离为线段AB的长画出即可；
（2）根据sin∠DBC=sin∠BCA，求出sin∠BCA的值即可得出答案．
点评：此题主要考查了图形的平移以及锐角三角函数的定义，根据锐角三角函数的性质得出sin∠DBC=sin∠BCA是解决问题的关键．
（2）在△ABC中，
AB=
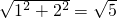，BC=，AC=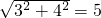．则AB2+BC2=AC2，
∴△ABC是直角三角形，∠ABC=90°
∴sin∠BCA=
∵线段BD是由线段AC平移得到的，
∴BD∥AC，
∴∠DBC=∠BCA，
∴sin∠DBC=sin∠BCA=
．分析：（1）直接平移A，C两点，再根据平移方向为射线AB的方向，平移的距离为线段AB的长画出即可；
（2）根据sin∠DBC=sin∠BCA，求出sin∠BCA的值即可得出答案．
点评：此题主要考查了图形的平移以及锐角三角函数的定义，根据锐角三角函数的性质得出sin∠DBC=sin∠BCA是解决问题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在平面直角坐标系中，动点P、Q同时从原点O出发，点P沿x轴正方向以每秒1个单位长度的速度运动，点Q沿y轴正方向以每秒3个单位长度的速度运动．过点P作x轴的垂线，分别交直线y=x+2、y=-x+1于C、D两点．分别以OQ、CD为边向右作正方形OQAB和正方形CDEF．
如图，在△ABC中，将△ABC沿x轴正方向平移2个单位长度，再沿y轴沿负方向平移1个单位长度得到△EFG．
)．
