题目内容
【题目】(数学实验)如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干个可以拼出一些长方形来解释某些等式.例如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.

(初步运用)
(1)仿照例子,图③可以解释为: ;
(2)取图①中的若干个(三种图形都要取到)拼成一个长方形,使它的边长分别为(2a+3b)、(a+5b),不画图形,试通过计算说明需要C类卡片多少张;
(拓展运用)
若取其中的若干个(三种图形都要取到)拼成一个长方形,使它的面积为2a2+5ab+3b2,通过操作你会发现拼成的长方形的长宽分别是 ,将2a2+5ab+3b2改写成几个整式积的形式为 .
【答案】(1)a2+2ab+b2;(2)15张;(3)2a+3b,a+b,(2a+3b)(a+b).
【解析】
(1)根据图②结合图形的面积即可得到结论;
(2)根据多项式乘多项式的法则即可得到结论;
(3)根据已知条件可画出图形,于是得到矩形的两边.
(1)图③可以解释为:(a+b)(a+b)=a2+2ab+b2;
故答案为:a2+2ab+b2;
(2)∵(2a+3b)(a+5b)=2a2+13ab+15b2,
∴需要C类卡片15张;
(3)如图:
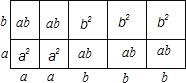
长方形的长是2a+3b,宽是a+b,2a2+5ab+3b2=(2a+3b)(a+b).
故答案为:2a+3b,a+b,(2a+3b)(a+b).

练习册系列答案
相关题目