题目内容
14.已知△ABC 中,a、b、c分别为∠A、∠B、∠C的对边,则下列条件中:①a=4,b=7$\frac{1}{2}$;c=8$\frac{1}{2}$;②a2:b2:C2=1:3:2;③∠A:∠B:∠C=3:4:5;④∠A=2∠B=2∠C.其中能判断△ABC是直角三角形的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 分别根据三角形内角和定理、勾股定理的逆定理对各选项进行逐一分析即可.
解答 解:①∵a2+b2=$\frac{289}{4}$=($\frac{17}{2}$)2,c2=(8$\frac{1}{2}$)2=($\frac{17}{2}$)2
∴a2+b2=c2,
∴此三角形是直角三角形,故本小题正确;
②∵a2:b2:c2=1:3:2,
∴设a2=x,则b2=3x,c2=2x,
∵x+2x=3x,
∴a2+c2=b2,
∴此三角形是直角三角形,故本小题正确;
③∵∠A:∠B:∠C=3:4:5,
∴设∠A=3x,则∠B=4x,∠C=5x.
∵∠A+∠B+∠C=180°,
∴3x+4x+5x=180°,
解得x=15°,
∴∠A=45°,∠B=60°,∠C=75°,
∴此三角形不是直角三角形,故本小题错误;
④∵∠A=2∠B=2∠C,
∴设∠B=∠C=x,则∠A=2x,
∴x+x+2x=180°,
解得:x=45°,
∴∠A=2x=90°,
∴此三角形是直角三角形,故本小题正确.
故选C.
点评 本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
5.下列运算正确的是( )
| A. | 2x2•x3=2x5 | B. | (x-2)2=x2-4 | C. | x2+x3=x5 | D. | (x3)4=x7 |
2.下列计算正确的是( )
| A. | 2-3=1 | B. | a2+2a2=3a4 | C. | 3×(-1)2=3 | D. | -|-3|=3 |
6.下列式子不是二次根式的是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{a}$(a≥0) | C. | $\sqrt{{a^2}+1}$ | D. | $\sqrt{-2}$ |
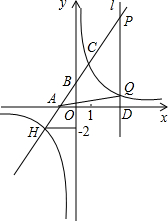 在平面直角坐标系xOy中,直线y=2x+2与x轴、y轴分别交于点A、B,与双曲线$y=\frac{k}{x}$交于第一象限的点C(1,m)和第三象限的点H,H点的纵坐标为-2
在平面直角坐标系xOy中,直线y=2x+2与x轴、y轴分别交于点A、B,与双曲线$y=\frac{k}{x}$交于第一象限的点C(1,m)和第三象限的点H,H点的纵坐标为-2