Question

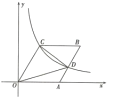
【题目】如图，在直角坐标系中，四边形OABC为菱形，OA在x轴的正半轴上，∠AOC=60°，过点C的反比例函数的图象与AB交于点D，则△COD的面积为（　　）

A.B.C.4D.

Answer 1

【答案】B

【解析】

易证S菱形ABCO=2S△CDO，再根据tan∠AOC的值即可求得菱形的边长，即可求得点C的坐标，可得菱形的面积和结论．

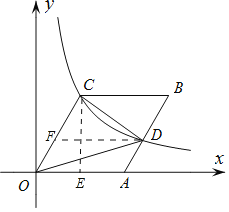
解：作DF∥AO，CE⊥AO，

∵∠AOC=60°，

∴tan∠AOC=，

∴设OE=x，CE=x，

∴xx=4，

∴x=±2，

∴OE=2，CE=2，

由勾股定理得：OC=4，

∴S菱形OABC=OACE=4×2=8，

∵四边形OABC为菱形，

∴AB∥CO，AO∥BC，

∵DF∥AO，

∴S△ADO=S△DFO，

同理S△BCD=S△CDF，

∵S菱形ABCO=S△ADO+S△DFO+S△BCD+S△CDF，

∴S菱形ABCO=2（S△DFO+S△CDF）=2S△CDO=8，

∴S△CDO=4；

故选：B．