题目内容
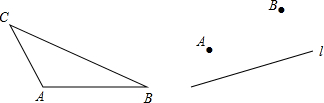
如图,已知∠A,请你仅用尺规,按下列要求作图和计算(不必写画法):(1)选取适当的边长,在所给的∠A图形上画一个含∠A 的直角三角形ABC,并标上字母,其中点C为直角顶点,点B为另一锐角顶点;
(2)以AC为一边作等边△ACD;
(3)若设∠A=30°、BC边长为a,则BD的长为______

【答案】分析:(1)在一边上任取一点C,然后过点C作AC的垂线与另一边相交于点B,则△ABC即为所求作的三角形;
(2)分别以A、C为圆心,以AC长为半径画弧,相交于点D,连接AD、CD则△ACD即为所求作的等边三角形;
(3)根据30°角所对的直角边等于斜边的一半求出AB的长度,再利用勾股定理求出AC的长度,然后分两种情况①点D在AC的下方时,作DE⊥BC交BC的延长线于点E,求出DE、CE的长度,然后求出BE的长度,再利用勾股定理列式计算即可得解,②点D在AC的上方时,求出∠BAD=30°,根据等边三角形的性质可得AB⊥CD,再根据对称性可得△ABD与△ABC关于AB成轴对称,根据轴对称的性质可得BD=BC.
解答: 解:(1)如图所示,△ABC为所求作的直角三角形(答案不唯一);
解:(1)如图所示,△ABC为所求作的直角三角形(答案不唯一);
(2)如图所示,△ACD为所求作的等边三角形,有点D在AC的上方与下方两种情况;
(3)∵∠A=30°、BC边长为a,
∴AB=2BC=2a,
根据勾股定理,AC= =
= =
= a,
a,
①点D在AC的下方时,作DE⊥BC交BC的延长线于点E,
则DE= AC=
AC= a,CE=
a,CE= a•sin60°=
a•sin60°= a×
a× =
= a,
a,
所以,BE=BC=CE=a+ a=
a= a,
a,
在Rt△BDE中,BD= =
= =
= a;
a;
②点D在AC的上方时,∵∠A=30°,
∴∠BAD=60°-30°=30°,
∴∠BAC=∠BAD,
∴AB⊥CD,
∴△ABD与△ABC关于AB成轴对称,
∴BD=BC,
∵BC=a,
∴BD=a;
综上所述,BD的长度为 a或a.
a或a.
故答案为: a或a.
a或a.
点评:本题考查了复杂作图,主要利用了过一点作已知直线的垂线,已知一边作等边三角形,都是基本作图,(3)题要注意分点D在AC的上方与下方两种情况讨论求解.
(2)分别以A、C为圆心,以AC长为半径画弧,相交于点D,连接AD、CD则△ACD即为所求作的等边三角形;
(3)根据30°角所对的直角边等于斜边的一半求出AB的长度,再利用勾股定理求出AC的长度,然后分两种情况①点D在AC的下方时,作DE⊥BC交BC的延长线于点E,求出DE、CE的长度,然后求出BE的长度,再利用勾股定理列式计算即可得解,②点D在AC的上方时,求出∠BAD=30°,根据等边三角形的性质可得AB⊥CD,再根据对称性可得△ABD与△ABC关于AB成轴对称,根据轴对称的性质可得BD=BC.
解答:
 解:(1)如图所示,△ABC为所求作的直角三角形(答案不唯一);
解:(1)如图所示,△ABC为所求作的直角三角形(答案不唯一);(2)如图所示,△ACD为所求作的等边三角形,有点D在AC的上方与下方两种情况;
(3)∵∠A=30°、BC边长为a,
∴AB=2BC=2a,
根据勾股定理,AC=
 =
= =
= a,
a,①点D在AC的下方时,作DE⊥BC交BC的延长线于点E,
则DE=
 AC=
AC= a,CE=
a,CE= a•sin60°=
a•sin60°= a×
a× =
= a,
a,所以,BE=BC=CE=a+
 a=
a= a,
a,在Rt△BDE中,BD=
 =
= =
= a;
a;②点D在AC的上方时,∵∠A=30°,
∴∠BAD=60°-30°=30°,
∴∠BAC=∠BAD,
∴AB⊥CD,
∴△ABD与△ABC关于AB成轴对称,
∴BD=BC,
∵BC=a,
∴BD=a;
综上所述,BD的长度为
 a或a.
a或a.故答案为:
 a或a.
a或a.点评:本题考查了复杂作图,主要利用了过一点作已知直线的垂线,已知一边作等边三角形,都是基本作图,(3)题要注意分点D在AC的上方与下方两种情况讨论求解.

练习册系列答案
相关题目
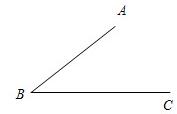 23、如图,已知∠ABC.请你再画一个∠DEF,使DE∥AB,EF∥BC,且DE交BC边与点P.探究:∠ABC与∠DEF有怎样的数量关系?并说明理由.
23、如图,已知∠ABC.请你再画一个∠DEF,使DE∥AB,EF∥BC,且DE交BC边与点P.探究:∠ABC与∠DEF有怎样的数量关系?并说明理由.
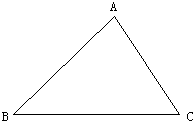 20、如图,已知△ABC,请你按要求用尺规作出下列图形(不写作法,但要保留作图痕迹).
20、如图,已知△ABC,请你按要求用尺规作出下列图形(不写作法,但要保留作图痕迹). 如图,已知∠A,请你画出△ABC的角平分线AD,中线AE,高线AF.此时图中除△ABC外,还有多少个三角形?
如图,已知∠A,请你画出△ABC的角平分线AD,中线AE,高线AF.此时图中除△ABC外,还有多少个三角形?