题目内容
4.已知⊙O的周长等于6πcm,则它的内接正六边形面积为$\frac{27\sqrt{3}}{2}$cm3.分析 首先过点O作OH⊥AB于点H,连接OA,OB,由⊙O的周长等于6πcm,可得⊙O的半径,又由圆的内接多边形的性质,即可求得答案.
解答 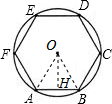 解:如图,过点O作OH⊥AB于点H,连接OA,OB,
解:如图,过点O作OH⊥AB于点H,连接OA,OB,
∴AH=$\frac{1}{2}$AB,
∵⊙O的周长等于6πcm,
∴⊙O的半径为:3cm,
∵∠AOB=$\frac{1}{6}$×360°=60°,OA=OB,
∴△OAB是等边三角形,
∴AB=OA=3cm,
∴AH=$\frac{3}{2}$cm,
∴OH=$\sqrt{O{A}^{2}-A{H}^{2}}$=$\frac{3\sqrt{3}}{2}$(cm),
∴S正六边形ABCDEF=6S△OAB=6×$\frac{1}{2}$×3×$\frac{3\sqrt{3}}{2}$=$\frac{27\sqrt{3}}{2}$(cm2).
故答案为;$\frac{27\sqrt{3}}{2}$.
点评 本题考查的是正多边形和圆,熟知正六边形的半径与边长相等是解答此题的关键.

练习册系列答案
相关题目
15. 如图所示,该几何体的俯视图是( )
如图所示,该几何体的俯视图是( )
 如图所示,该几何体的俯视图是( )
如图所示,该几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
16.2014年11月份,某市区一周空气质量报告中某污染指数的数据是:61,75,61,63,50,63,61,则下列表述错误的是( )
| A. | 方差是44 | B. | 众数是61 | C. | 平均数是62 | D. | 中位数是61 |
13.三个非零实数a、b、c,满足a>b>c,且a+b+c=0,则下列不等式一定正确的是( )
| A. | ac<bc | B. | bc>c2 | C. | ab>b2 | D. | a2<b2 |
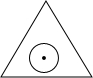 如图,一个半径为r的圆形纸片在边长为a(a≥2$\sqrt{3}$r)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是$(3\sqrt{3}-π){r}^{2}$.
如图,一个半径为r的圆形纸片在边长为a(a≥2$\sqrt{3}$r)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是$(3\sqrt{3}-π){r}^{2}$.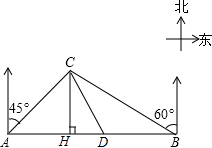 某大草原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H.
某大草原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H.